Οι Ermentrout & Cowan λένε ότι οι οπτικές εντυπώσεις γοητεύουν τους ανθρώπους αιώνες τώρα, αλλά μόνο πρόσφατα οι επιστήμονες ξεκίνησαν να ερευνούν τις μορφές και τους μηχανισμούς τους. Οι οπτικές εντυπώσεις συναντώνται σε ποικιλία διαφορετικών καταστάσεων: Σε περιπτώσεις επιληψίας, υπναγωγών παραισθήσεων, ημικρανιών, παραισθήσεων λόγω χρήσης ναρκωτικών κτλ., αλλά και σε πνευματικές εμπειρίες. Αυτές οι περιπτώσεις χαρακτηρίζονται από την εμφάνιση πολλών απλών γεωμετρικών δομών που είναι ανεξάρτητες από πλαίσιο και προηγούμενη εμπειρία.

Καμία προσπάθεια ταξινόμησης των μορφών των απλών οπτικών εντυπώσεων δεν έχει γίνει πριν το 1966, που ο Kluver ξεκίνησε σειρά εκτεταμένων πειραμάτων. Παρατήρησε ότι ανεξάρτητα από την αιτία της αισθητηριακής διαταραχής, σχεδόν όλες οι απλές οπτικές εντυπώσεις μπορούν να ταξινομηθούν σε μια από τις πιο κάτω τέσσερις κατηγορίες ‘σταθερών μορφών’: (1) Σχάρα, δικτυωτό, μαίανδρος, κυψέλη, σκακιέρα. (2) Ιστός αράχνης. (3) Χωνί, τούνελ, κώνος. (4) Σπιράλ. Η τάση προς τη γεωμετρικοποίηση, όπως εκφράζεται σε αυτές τις σταθερές μορφές, είναι επίσης προφανής με τους εξής δύο τρόπους: (1) Οι μορφές επαναλαμβάνονται, συνδυάζονται ή γίνονται αντικείμενο επεξεργασίας σε διακοσμητικά σχέδια και μωσαϊκά διαφόρων ειδών. (2) Τα στοιχεία που συνιστούν τις μορφές έχουν όρια που αποτελούνται από γεωμετρικά σχήματα.

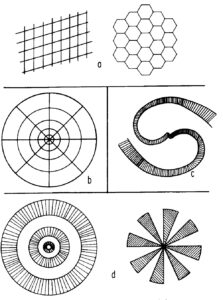
Τα πρότυπα είναι κυρίως δύο τύπων: Μικρά επαναλαμβανόμενα ‘μωσαϊκά’ (μορφές a και b) και πιο ‘ολιστικά’ μοτίβα (c, d). Στην εικόνα 1a βλέπουμε εντυπώσεις δικτυωτού που χαρακτηρίζονται από μικρές επαναλαμβανόμενες γεωμετρικές διακοσμήσεις του οπτικού χώρου με ψηφιδωτό. Η εικόνα 1b απεικονίζει μια τυπική εντύπωση ιστού αράχνης. Με κάποια έννοια είναι παρόμοια με την εικόνα 1a, μόνο που είναι διαφοροποιημένη. Η εικόνα 1d δείχνει δύο τύπους εντυπώσεων ‘τούνελ’ ή ‘χωνί’. Τέλος, μια τυπική μορφή σπιράλ απεικονίζεται στην εικόνα 1c. Φυσικά υπάρχουν παραλλαγές και συνδυασμοί όλων αυτών.  

< Σχήμα 1. a Τυπικό δικτυωτό, b Ιστός αράχνης, c Σπιράλ, d Τούνελ και χωνί >

Το επόμενο λογικό ερώτημα είναι από πού προέρχονται οι οπτικές εντυπώσεις. Κάποιοι πειραματιστές πιστεύουν ότι οι οπτικές εντυπώσεις συμβαίνουν ως αποτέλεσμα της επίδρασης του φωτός που πέφτει σε διάφορες δομές στο μάτι: Οι μορφές δικτυωτού μπορεί να οφείλονται στη δικτύωση των αγγείων εντός του ματιού. Ωστόσο, πειράματα που έγιναν στο απόλυτο σκοτάδι, και στα οποία τα υποκείμενα έχουν οπτικές εντυπώσεις, καταρρίπτουν αυτή τη θεωρία. Αυτά τα πειράματα, σε συνδυασμό με την πλούσια φαντασία που εμφανίζεται στα ύστερα στάδια των εντυπώσεων, συνεπάγονται ότι πηγή των απλών μοτίβων είναι διαδικασίες του εγκεφαλικού φλοιού και όχι των περιφερειακών οργάνων.

Υποθέτοντας ότι οι οπτικές εντυπώσεις είναι φλοιϊκές στην προέλευσή τους αναζητούνται οι πιθανές αιτίες των διαταραχών που δημιουργούν αυτά τα μοτίβα. Οι ερευνητές ισχυρίζονται ότι μια αύξηση στον φλοιϊκό ερεθισμό είναι απαραίτητη για να ξεκινήσουν αυτές οι εντυπώσεις. Πρέπει να υπάρχουν -εκτός από τις αρχικά αναφερόμενες- και άλλες επιρροές που διαμορφώνουν τον φλοιϊκό ερεθισμό, ωστόσο για τη φύση αυτών των επιρροών λίγα είναι σήμερα γνωστά.

Τα πιο πάνω πειραματικά στοιχεία οδηγούν στη βασική υπόθεση ότι οι απλές εντυπώσεις εμφανίζονται εξαιτίας μιας αστάθειας/ ανισορροπίας στην κατάσταση ηρεμίας που οδηγεί σε ακόλουθα χωρικά μοτίβα δραστηριότητας στον φλοιό. Η αστάθεια εμφανίζεται από ένα συνδυασμό αυξημένης διέγερσης και μειωμένης αναστολής.

Μπορούμε να ταξινομήσουμε τις σταθερές μορφές των οπτικών εντυπώσεων σε δυο κύριες κλάσεις: (i) Βασικά πρότυπα που συνίστανται από εξάγωνα, οκτάγωνα, τετράγωνα και ορθογώνια και (ii) στρογγυλές μορφές που συνίστανται από σταθερά πρότυπα και δείχνουν προς κάποια κατεύθυνση. Και οι δυο κλάσεις, από μαθηματική άποψη, εμφανίζουν πρότυπα διπλής περιοδικότητας στο επίπεδο. 

Οι παράμετροι φυσιολογίας του εγκεφάλου παίζουν σημαντικό ρόλο στην επιλογή των σταθερών μορφών, αλλά αυτές οι παράμετροι δεν συνιστούν από μόνες τους επαρκή εξήγηση για την εμφάνιση αυτών των μορφών. Αυτός ο μηχανισμός επιλογής είναι δυναμικός και κάτω από αυτή την επιλογή των σταθερών μορφών βρίσκονται οι ιδιότητες της σταθερότητας. 

Εδώ αναφερόμαστε σε απλές οπτικές εντυπώσεις, αλλά, καθώς τα στάδια οραματισμού προχωράνε συνεχώς, εμπλέκονται περισσότερο οι μηχανισμοί που εδράζουν στον φλοιό και εμφανίζονται πιο σύνθετες μορφές που εξαρτώνται από το πλαίσιο. Σήμερα οι ερευνητές επικαλούνται μια τέτοια σύνθετη διαδικασία για να ερμηνεύσουν την πανταχού παρουσία απλών μωσαϊκών και γεωμετρικών προτύπων. Είναι, όμως, πιθανώς μη αναγκαίο κάτι τέτοιο, αν υποθέσουμε ότι υπό φυσιολογικές συνθήκες οι οπτικές εντυπώσεις που παρουσιάζονται χωρίς οποιουδήποτε είδους εξωτερικούς ερεθισμούς είναι προϊόν του ασυνειδήτου και συνεπώς ανάγονται σε διαδικασίες του παλαιο-εγκέφαλου και όχι του νεο-εγκέφαλου, δηλαδή του φλοιού. 

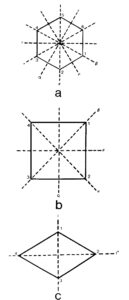
Τέλος, ένα βασικό θέμα αυτών των σχεδίων είναι η ύπαρξη συμμετριών όπως αυτές φαίνονται πιο κάτω: a Εξαγωνική, b Τετραγωνική, c Ρομβική. Σε αυτές πρέπει να προσθέσουμε και την κυκλική.

     Σχήμα 2. Βασικές ομάδες συμμετρίας. a Εξαγωνική, b Τετραγωνική, c Ρομβική >

Ο Gontar αναφέρει ότι σύμφωνα με τον Jung, το mandala ως ψυχολογικό φαινόμενο εμφανίζεται αυθόρμητα στα όνειρα, σε συγκεκριμένες καταστάσεις εσωτερικής σύγκρουσης και σε περιπτώσεις σχιζοφρένειας. Πολύ συχνά περιλαμβάνει μια τετράδα ή ένα πολλαπλάσιο του τέσσερα, με τη μορφή σταυρού, αστεριού, ή τετραγώνου, οκταγώνου κτλ. Το γεγονός ότι οι εικόνες (mandala) αυτού του είδους έχουν υπό ορισμένες προϋποθέσεις σημαντική θεραπευτική επίδραση στους δημιουργούς τους αποδεικνύεται εμπειρικά και γίνεται εύκολα κατανοητό, κατά το ότι συχνά αναπαριστούν πολύ έντονες προσπάθειες να διακριθούν και να τεθούν μαζί προφανώς ασυμφιλίωτα αντίθετα και να γεφυρωθούν εμφανώς αγεφύρωτα χάσματα. Ακόμα και η απλή προσπάθεια προς αυτή την κατεύθυνση συνήθως έχει θεραπευτική επίδραση, αλλά όταν γίνεται αυθόρμητα. Τίποτα δεν μπορεί να αναμένεται από μια τεχνητή επανάληψη ή ηθελημένη μίμηση τέτοιων εικόνων.

Η προτεινόμενη θεωρητική προσέγγισή του βασίζεται στη χρήση στοιχειωδών φυσικών αρχών για τη δυναμική βιοχημικών αντιδράσεων. Το αντίστοιχο μαθηματικό μοντέλο, που προέρχεται από αυτές τις αρχές, αντανακλά τους φυσικούς περιορισμούς για τη δυναμική των βιοχημικών αντιδράσεων και επομένως πρέπει να έχει υψηλό επίπεδο πρόβλεψης. Η υπόθεση ότι η κατανομή των συγκεντρώσεων των χημικών στους εγκεφαλικούς νευρώνες αντιστοιχεί ή με κάποιο τρόπο σχετίζεται με τις διαδικασίες εγκεφαλικής δημιουργικότητας, βρίσκει επιβεβαίωση από τη δημιουργία γενικευμένων προτύπων με μορφή mandala.

Σύμφωνα με τους Bressloff et al., το να βλέπει κάποιος ζωντανές οπτικές εντυπώσεις είναι μια εμπειρία που περιγράφεται σε όλους τους ανθρώπινους πολιτισμούς. Ζωγραφισμένες εικόνες βρίσκονται σε προϊστορικές σπηλιές και είναι αποτυπωμένες σε πετρογλυφικά. Τις οπτικές εντυπώσεις μπορεί να τις δει κάποιος κάτω από διάφορες συνθήκες: Κατά τη διάρκεια του ύπνου και κατά τον ξύπνο, έχοντας αισθητηριακή αποστέρηση, μετά από λήψη αναισθητικών, μετά από έντονο φως που αναβοσβήνει ή εφαρμόζοντας βαθιά πίεση και στα δύο μάτια, σε εμπειρίες επιθανάτιες και, το πιο σημαντικό, αμέσως μετά τη λήψη παραισθησιογόνων που περιέχουν συστατικά όπως το LSD, η κάνναβη, η μεσκαλίνη ή η ψιλοσυμβίνη. Στις περισσότερες περιπτώσεις τις εικόνες τις βλέπει κάποιος και στα δύο μάτια και κινούνται με αυτά, αλλά διατηρούν τις σχετικές θέσεις στο οπτικό πεδίο, γεγονός που ερμηνεύεται ότι γεννιούνται στον εγκέφαλο. Μια πιθανή θέση για την προέλευσή τους παρέχεται από μελέτες fMRI της οπτικής φαντασίας που υποθέτουν ότι η περιοχή V1 του εγκεφάλου ενεργοποιείται όταν τα υποκείμενα καθοδηγούνται να διερευνήσουν τις λεπτομέρειες ενός φανταστικού οπτικού αντικειμένου.

Τέτοιες εικόνες βλέπουν και τα τυφλά υποκείμενα καθώς και υποκείμενα κλεισμένα σε σφραγισμένα σκοτεινά δωμάτια. Διάφορες αναφορές δείχνουν ότι, αν και είναι δύσκολο να τοποθετηθούν στον χώρο και στην πραγματικότητα κινούνται μαζί με τα μάτια, οι  σχετικές μεταξύ τους θέσεις παραμένουν σταθερές σε αντιστοιχία με τέτοιες κινήσεις. Αυτό συνεπάγεται ότι δεν δημιουργούνται στα μάτια, αλλά κάπου στον εγκέφαλο. Ένα στοιχείο για τη θέση τους στον εγκέφαλο παρέχεται από σύγχρονες μελέτες της οπτικής φαντασίας. Αν και αμφιλεγόμενα, τα στοιχεία φαίνεται να υποθέτουν ότι οι περιοχές V1 και V2, o ραβδωτός και ο υπερ-ραβδωτός (striate and extra– striate) οπτικός εγκέφαλος, εμπλέκονται στην οπτική φαντασία, ιδιαίτερα αν η εικόνα απαιτεί  λεπτομερή έλεγχο. Πιο συγκεκριμένα, έχει προταθεί ότι η τοπολογική αναπαράσταση (που παρέχεται από την περιοχή V1) μπορεί να υποβοηθήσει την οπτική φαντασία όταν το υποκείμενο εξετάζει λεπτομερώς και με προσοχή τοπικά χαρακτηριστικά των αντικειμένων που αποθηκεύονται στη μνήμη.

Έτσι η οπτική φαντασία αντιμετωπίζεται ως το αποτέλεσμα της αλληλεπίδρασης μεταξύ των μηχανισμών που εξυπηρετούν την ανάκληση οπτικών αναμνήσεων και εκείνων που περιλαμβάνουν την εστιακή προσοχή. Από αυτή την άποψη είναι ενδιαφέρον το ότι φαίνεται να υπάρχει ανταγωνισμός μεταξύ του να βλέπει κάποιος οπτικές φαντασίες και οπτικές εντυπώσεις: «Αφότου μια εικόνα τοποθετήθηκε στο φόντο και μετά μετακινήθηκε, προσπάθησα να την δω με ανοιχτά μάτια. Δεν τα κατάφερα σε καμία περίπτωση. Μόνο (ψευδαισθησιακά) οπτικά φαινόμενα κάλυπταν το αντικείμενο».

Πηγές Πληροφορίας

• Klüver, H. (1966). Mescal and mechanisms of hallucinations. University of Chicago Press, Chicago.

• Ermentrout, G. B. & Cowan, J. D. (1979). A Mathematical Theory of Visual Hallucination Patterns. Biol. Cybernetics 34, 137-150.

• Gontar, V. (2000). Theoretical Foundation for Jung’s “Mandala Symbolism” Based on Discrete Chaotic Dynamics of Interacting Neurons. Discrete Dynamics in Nature and Society 5(1), 19-28.

• Bressloff, P. C., Cowan, J. D., Golubitsky, M., Thomas, P. J., & Wiener, M. C. (2001). Geometric visual hallucinations, Euclidean symmetry, and the functional architecture of striate cortex. Trans. Roy. Soc. Lond. B, 356, 299–330.

• Bressloff, P. C., Cowan, J. D., Golubitsky, M., Thomas, P. J., & Wiener, M. C. (2002). What Geometric Visual Hallucinations Tell Us about the Visual Cortex.  Neural Computation, 14(3), 473-491, MIT Press, Cambridge, MA.  

• Jung, C. G. (1972). Mandala Symbolism. Princeton University Press, Princeton, NJ.

• Longchenpa (2000). You Are the Eyes of the World. Snow Lion Publ., Ithaca, NY.