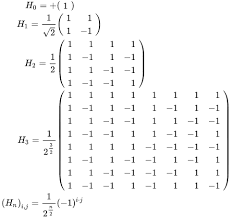Στο παρόν κείμενο παρουσιάζεται η ομοιότητα της δημιουργικής πράξης στα Μαθηματικά και στην Τέχνη, κυρίως την Ποίηση, από τη σκοπιά πολλών αξιόλογων δημιουργών και των δυο πεδίων.
Η λέξη Τέχνη χρησιμοποιείται ως γενικός όρος για διάφορους κλάδους της γνώσης: Λογοτεχνία -εδώ κυρίως Ποίηση-, μουσική, πλαστικές τέχνες κλπ. Βεβαίως, μεταξύ Μαθηματικών και Τέχνης υπάρχουν ουσιαστικές διαφορές, τις οποίες κάθε μορφωμένο άτομο μπορεί να λάβει υπόψη του. Κανένας δεν μπερδεύει ποτέ ένα θεώρημα των Μαθηματικών με ένα τραγούδι του Schubert ή έναν πίνακα του Van Gogh. Παρά τις προφανείς διακρίσεις, μπορεί να διαπιστωθεί ισχυρή και εκπληκτική σχέση μεταξύ Μαθηματικών και Τέχνης. Ο καθοριστικός παράγοντας αυτής της σχέσης είναι, κατά τη γνώμη του μαθηματικού και φιλόσοφου Imre Tóth, αυτός που «στη φαινομενολογία του πνεύματος, Τέχνη και Μαθηματικά ανταγωνίζονται να επιτύχουν τον ίδιο ένδοξο στόχο: να ξυπνήσουν το πνεύμα στην αυτογνωσία της δημιουργικής πράξης».
Είναι πράγματι αλήθεια ότι η πράξη δημιουργίας είναι πιο εντυπωσιακά παρούσα στην Τέχνη, αλλά για τους μαθηματικούς και τους λογικολόγους υψηλού επιπέδου, η δημιουργική πράξη είναι ομοίως ορατή και στα Μαθηματικά. Επιπλέον, η μαθηματική δημιουργία και η καλλιτεχνική δημιουργία αντιπροσωπεύουν γι’ αυτές τις προσωπικότητες παρόμοιες πνευματικές δραστηριότητες. Ο Imre Tóth δηλώνει την ίδια αρχή στη μελέτη του Achilles: «Η διαδικασία της δημιουργίας αναπτύσσεται στον πνευματικό κόσμο, αρχικά με αυθόρμητο τρόπο. Σε όλα τα πεδία όπου δημιουργούνται νοητικά αντικείμενα, και ειδικά στα Μαθηματικά, το πνεύμα που ασχολείται με τη μόνιμη και αδιάκοπη πράξη της δημιουργίας/ γένεσης, διαδίδεται και πολλαπλασιάζεται ως πλούσια βλάστηση, γεμίζοντας συνεχώς τον χώρο με τις δικές του δημιουργίες. Ο ίδιος ο μαθηματικός ή ο καλλιτέχνης αποκαλύπτει τον εαυτό του ως τυφλή δύναμη της Φύσης, όπως η ίδια η Φύση, που δημιουργεί και δημιουργείται μέσα από την ανεμπόδιστη ασυνειδητότητα, γεννά και γεννιέται χωρίς να το γνωρίζει αυτό». Συχνά λέγεται ότι η διαίσθηση και η φαντασία κατέχουν την πρώτη θέση στην Τέχνη, ενώ στα Μαθηματικά, η λογική και η αυστηρότητα κατέχουν το προσκήνιο, επενδύοντας το μαθηματικό σύμπαν με ψυχρότητα και μη φιλικότητα, μια κατάσταση μάλλον ξένη προς τον άνθρωπο, για τον οποίο η Τέχνη είναι πολύ πιο οικεία. Κάτι τέτοιο συμβαίνει πραγματικά; Η κατάσταση είναι πολύ πιο περίπλοκη στην πραγματικότητα, Τέχνη και Μαθηματικά δεν είναι τόσο άκαμπτα διαχωρισμένα, όντας μάλλον έντονα συνδεδεμένα.
Ας λάβουμε υπόψη τις ιδέες του Αμερικανού μαθηματικού Marston Morse (1892-1977) που παρατηρεί ότι «η πρώτη κύρια σχέση μεταξύ Μαθηματικών και Τέχνης έγκειται στο γεγονός ότι η ανακάλυψη στα Μαθηματικά δεν είναι θέμα λογικής, αλλά μάλλον το αποτέλεσμα μερικών θαυμαστών δυνάμεων που κανένας δεν μπορεί να καταλάβει και όπου η ασυνείδητη αναγνώριση της ομορφιάς οφείλει να διαδραματίζει σημαντικό ρόλο. Από ένα μεγάλο πλήθος από μοτίβα, ο μαθηματικός επιλέγει ένα δείγμα, για λόγους ομορφιάς, και το ‘φυτεύει’, χωρίς να το γνωρίζει κανένας. Στη συνέχεια, η λογική των όρων και των σχημάτων τοποθετεί το μοτίβο σε προσιτή θέση. Μόνο τώρα είναι δυνατό να το κοινωνήσει στους άλλους. Το μοτίβο εντυπώνεται στη μνήμη κάποιου». Δεν υπάρχει αμφιβολία ότι ο Marston Morse, ως μεγάλος δημιουργός, γνώριζε για τι μιλούσε.
Υπάρχουν πολλές ευκαιρίες να πεισθούμε ότι η φαντασία και η διαίσθηση, η λογική και η αυστηρότητα αντιπροσωπεύουν χαρακτηριστικά που μπορούν να συνδεθούν εξίσου με τον μαθηματικό και τον καλλιτέχνη. Ο Marston Morse ισχυρίζεται αξιόπιστα ότι «τα Μαθηματικά είναι η αδελφή και ο απαραίτητος βοηθητικός κλάδος της Τέχνης και τον αγγίζει η τρέλα και η μεγαλοφυΐα». Αυτό το πλαίσιο τον φέρνει πιο κοντά στον άγγλο φιλόσοφο και μαθηματικό Alfred North Whitehead, κατά την άποψη του οποίου “Η επιδίωξη των Μαθηματικών είναι μια θεϊκή τρέλα του ανθρώπινου πνεύματος”. Οι δρόμοι τους έρχονται σε επαφή με την Ποίηση με την έννοια του Πλάτωνα: “η Ποίηση είναι μια θεϊκή τρέλα”. Φαίνεται ως να έχει καταστρατηγηθεί εδώ η λέξη ‘τρέλα’, αλλά δεν πρέπει να υπάρχει αμφιβολία ότι οι μαθηματικοί θεωρούν τη μαθηματική τρέλα ως μια ενεργητική/ δημιουργική φαντασία -προφανώς καθαυτή απεριόριστη, αλλά περιοριζόμενη από την αρχή της μη- αντίφασης, που παρέχει τη μεγάλη ευκαιρία της αλήθειας-, η οποία επιτρέπει στον μαθηματικό να δημιουργήσει έναν αφηρημένο και αυτόνομο κόσμο, που ανήκει εξ ολοκλήρου στο σύμπαν της σκέψης και που, ακριβώς λόγω του υψηλού βαθμού γενικότητας και αφαίρεσής του, τον κάνει ικανό να την εφαρμόσει στον κόσμο της ύλης και της αίσθησης.
Ο αλγεβριστής Leopold Kronecker κάποτε παρατηρούσε: «Δεν είναι οι μαθηματικοί πραγματικοί και γνήσιοι ποιητές; Πράγματι είναι, ακριβώς όμως οι παραστάσεις τους πρέπει να αποδειχθούν». Ο Kronecker παρατηρεί ότι τα Μαθηματικά είναι ποιητικά, αλλά προσθέτει ότι διαφέρουν ως προς το ότι πρέπει να αποδειχθούν οι μέθοδοι τους -μια αναφορά στο μαθηματικό βήμα-προς-βήμα στυλ θεωρητικής έκθεσης, ιδιαίτερα στην απόδειξη. Ένας άλλος μαθηματικός, που κάποτε στράφηκε στην ποίηση, είναι ο Felix Hausdorff, ο οποίος έκανε σημαντικές προόδους στην Τοπολογία και στη Θεωρία Συνόλων. Με το ψευδώνυμο Paul Mongré δημοσίευσε μυθιστόρημα, φιλοσοφία, θεατρικά έργα και ποίηση. Η μεγάλη συλλογή ποίησής του, Ekstases, δημοσιεύθηκε το 1900 και ασχολείται με τη «φύση, τη ζωή, τον θάνατο και το ερωτικό πάθος».
Η δήλωση ότι η φαντασία ενός ιδιοφυούς μαθηματικού μπορεί να ανταγωνιστεί εκείνη ενός Σαλβαδόρ Νταλί δεν πρέπει να αποτελεί έκπληξη. Το γεγονός αυτό επιβεβαιώνεται από τους Καντοριανούς τακτικούς αριθμούς, τις μη Ευκλείδειες Γεωμετρίες, τα μη συμβατικά σύμπαντα και από τόσες άλλες μαθηματικές οντότητες που αμφισβητούν τη γενική διαίσθηση –για παράδειγμα, την καμπύλη του Peano που ‘γεμίζει’ ένα τετράγωνο, την ταινία του Möbius, ένα αξιοσημείωτο παράδειγμα μονοπρόσωπης επιφάνειας, τα μορφοκλασματικά του Mandelbrot κτλ. Στην εργασία του Creation poetique et création scientifique, ο Γάλλος βιολόγος Jean Bernard διακρίνει σαφώς μεταξύ των δύο τύπων δημιουργίας, στηρίζοντας τον ισχυρισμό του στη διάκριση μεταξύ των δύο όρων: ανακάλυψη και εφεύρεση, όσον αφορά την πρώτη ως έναν όρο ειδικό για την Επιστήμη και τον δεύτερο ως ειδικό για την Τέχνη. Ο Γάλλος μαθηματικός Jacques Hadamard (1865-1963) στο έργο του The Psychology of Invention in the Mathematical Field, (Η Ψυχολογία της Επινόησης στα Μαθηματικά), πιστεύει ότι οι δύο όροι συνδέονται στενά και, επιπλέον, από ψυχολογική άποψη, δεν υπάρχει διάκριση μεταξύ τους.
Ο Hadamard επισύρει επίσης την προσοχή μας όταν, ξεκινώντας από μια επιστολή που απηύθυνε ο Μότσαρτ στην αδελφή του, όπου ο αυστριακός συνθέτης αναλύει ολόκληρη τη δημιουργική πράξη του, φτάνει στο συμπέρασμα ότι η διαδικασία της δημιουργίας είναι πανομοιότυπη και διέρχεται από παρόμοια στάδια στα Μαθηματικά και στην Τέχνη. Αυτά τα στάδια είναι τα ακόλουθα:
(i) συνειδητή προετοιμασία˙ (ii) επώαση˙ (iii) φώτιση/ έμπνευση˙ (iv) ολοκλήρωση (συνειδητό και ορθολογικό στάδιο επαλήθευσης, που βάζει τις τελευταίες πινελιές σε μια θεωρία).
Ένας άλλος αντιπροσωπευτικός Γάλλος μαθηματικός, ο Henri Poincaré (1854-1912), καταλήγει στο ίδιο συμπέρασμα, υπογραμμίζοντας τη στιγμή της φώτισης, ως μια στιγμή της εξεύρεσης απροσδόκητα της λύσης σε ένα συγκεκριμένο πρόβλημα, προσφέροντας ως παράδειγμα την προσωπική του ανακάλυψη, όταν διατύπωσε τη θεμελιώδη ιδέα της θεωρίας των συναρτήσεων Fuchsian: «Ένα πρωί, περπατώντας δίπλα στον βράχο, ξαφνικά έλαμψε στο μυαλό μου η ιδέα ότι οι αριθμητικοί μετασχηματισμοί των αόριστων τετραγωνικών μορφών είναι πανομοιότυποι με εκείνους της μη Ευκλείδειας Γεωμετρίας» (The Poincaré Work on Fuchsian Functions). Το ίδιο συμβαίνει και με τη δημιουργική πράξη στην Τέχνη, όπως ομολογούν οι Μότσαρτ, Lamartine και Paul Valéry.
Είναι πολύ ενδιαφέρον και σπουδαίο το γεγονός ότι τόσο ο Paul Valéry όσο και ο Poincaré, ποιητής και μαθηματικός αντίστοιχα, θεωρούν ότι η πράξη της δημιουργίας εξαρτάται από δύο βασικές λειτουργίες: συνδυασμούς και επιλογές, με την τελευταία να είναι η ουσιαστική, καθώς αυτή ‘ορίζει’ τη μεγαλοφυΐα. Αυτές οι πτυχές και πολλές άλλες απόψεις, μελετώνται διεξοδικά από τον Solomon Marcus σε διάφορα έργα, όπου ο συγγραφέας ασχολείται διαρκώς με την ενσωμάτωση των Μαθηματικών στον οικουμενικό πολιτισμό, μέσω της δημιουργίας σημαντικών συνδέσεων μεταξύ των Μαθηματικών και άλλων τομέων του νου: Λογοτεχνία, Τέχνη, φιλοσοφία κλπ. Μια άλλη ενδιαφέρουσα, αλλά λιγότερο εκπληκτική πτυχή, είναι ότι οι μαθηματικοί δίνουν την απόδειξη ενός αληθινά λογοτεχνικού ταλέντου κάθε φορά που προσπαθούν να καταστήσουν το εννοιολογικό σύστημά τους προσιτό σε εκείνους που δεν διαθέτουν εξειδικευμένες γνώσεις Μαθηματικών. Ένα πρώτο παράδειγμα είναι το έργο του Imre Tóth: Achilles. The Eleatic Paradoxes in the Phenomenology of the Spirit (Αχιλλέας. Τα Ελεατικά Παράδοξα στη Φαινομενολογία του Πνεύματος), που αποτιμάται ως τριπλό αριστούργημα: μαθηματικό, φιλοσοφικό και λογοτεχνικό. Κατά τον ίδιο τον Imre Tóth: «Στην κανονική σχολαστική ταξινόμηση, που διακρίνει τις φυσικές επιστήμες και τις τέχνες, τα Μαθηματικά συνδέονται πάντοτε με τις φυσικές επιστήμες, αλλά κατά την άποψή μου η οντολογία και η επιστημολογία της μαθηματικής μάθησης μας οδηγούν να τα δούμε να συνδέονται με την Τέχνη. Επαναλαμβάνω: η μάθηση (Mathesis) και η Ποίηση (Poiesis) έχουν παρόμοιες οντολογικές δομές».
Αναφερόμενοι στον ποιητή Paul Valéry, να σημειώσουμε ότι είναι ένας από τους θαυμαστές του Mallarmé, στον οποίο γράφει: «Η Ποίηση μου φαίνεται σαν μια λεπτή, όμορφη εξήγηση του κόσμου. Ενώ η μεταφυσική τέχνη βλέπει το σύμπαν να κατασκευάζεται από καθαρές και απόλυτες ιδέες, και η ζωγραφική το βλέπει από την άποψη των χρωμάτων, η ποιητική τέχνη συνίσταται στο να το θεωρούμε επιστρωμένο με συλλαβές, οργανωμένο σε προτάσεις». Στο οποίο απαντάει ο Mallarmé: «Ναι, αγαπητέ ποιητή μου, για να κατανοήσουμε τη Λογοτεχνία και να έχουμε ένα λόγο γι’ αυτό, πρέπει να επιτύχουμε αυτή την ‘υψηλή συμφωνία’ που ίσως κανένας δεν θα δημιουργήσει˙ αλλά έχει στοιχειώσει ακόμα και τον λιγότερο συνειδητό από εμάς και τα κύρια χαρακτηριστικά της, χυδαία ή λεπτά, σφραγίζουν κάθε γραπτή εργασία».
Πολλοί μελετητές μεταφέρουν την έκφραση του Valéry και στα δυο πεδία, φτιάχνοντας μια θεωρία: Μαθηματικά και Ποίηση: ‘μια λεπτή, όμορφη εξήγηση του κόσμου’.
Η Growney, για παράδειγμα, δεν προσπαθεί πάντα να προωθήσει κάποια θεωρία για το πώς τα Μαθηματικά και η Ποίηση μπορεί να σχετίζονται, αλλά προτιμάει να προσφέρει τα ποιήματα όπως είναι, επισημαίνοντας ότι η χρήση της μαθηματικής ορολογίας και των μαθηματικών καλολογικών στοιχείων δημιουργεί μια ‘ιδιαίτερη ζωντάνια’. Υποδεικνύοντας ότι τέτοια στοιχεία/ εικόνες δεν θα μπορούσαν να μεταδοθούν εύκολα σε συνηθισμένη γλώσσα, καταλήγει: «οι ποιητές χρησιμοποιούν μαθηματικούς όρους για να μας δώσουν την εικόνα που αξίζει χίλιες λέξεις». Αυτή η παρατήρηση ενσωματώνει ένα σημαντικό σημείο αυτής της έρευνας: ότι τόσο τα Μαθηματικά όσο και η Ποίηση μοιράζονται μια συναισθηματική ποιότητα, που θα ήταν, χωρίς τη σύνθεσή τους, αδύνατο να περιγραφεί.
Η Growney, με βασική της ιδέα ότι τα Μαθηματικά επηρεάζουν/ εμπνέουν την Ποίηση, λέει τα εξής: «Άρχισα να συγκεντρώνω παραδείγματα Ποίησης με μαθηματικά καλολογικά στοιχεία/ σχήματα λόγου για να εμπλουτίσω τα μαθήματα των Μαθηματικών. Και η Ποίηση και τα Μαθηματικά χρησιμοποιούν συγκεντρωτική γλώσσα, δηλώνοντας με συνοπτική χάρη κάτι περισσότερο από αυτό που είναι προφανές. Σταδιακά έγινα συγγραφέας ποιημάτων και, μέσα σε αυτή τη δραστηριότητα, έψαχνα τις μαθηματικές επιρροές στη δομή της Ποίησης. Με βάση παραδείγματα από αυτές τις έρευνες, αναπτύσσω και επεξηγώ τα εξής σημεία:
(1) τα Μαθηματικά και η Ποίηση απαιτούν παρόμοια δημιουργικότητα˙
(2) οι περιορισμοί που αφορούν τα Μαθηματικά δίνουν στους ποιητές την ευκαιρία να ανακαλύψουν νέα γλώσσα˙
(3) τα Μαθηματικά παρέχουν ακριβή και ζωντανά σχήματα λόγου για τα ποιήματα».
Δεδομένου ότι γίνεται αναφορά στη λογοτεχνική ομορφιά ορισμένων μαθηματικά προσανατολισμένων κειμένων, το επόμενο απόσπασμα, που ανήκει στον Ελβετό μαθηματικό και φιλόσοφο Ferdinand Gonseth αξίζει να αναφερθεί: «Στην ουσία τους, τα Μαθηματικά δεν είναι τίποτα περισσότερο από μια συναρμογή από σχηματικές διαδικασίες και οράματα του πνεύματός μας, μια συνειδητή απάντηση στην ασυνείδητη δραστηριότητα που εφαρμόζει σε εμάς μια εικόνα του κόσμου και ένα μεγάλο μέρος των κανόνων που καθορίζουν τις πράξεις και τις αντιδράσεις μας. Δεν είναι ένα οικοδόμημα σταθερής θεμελίωσης, απόλυτης σταθερότητας, αλλά είναι μάλλον μια εναέρια κατασκευή που κρατά με θαυματουργό τρόπο τη δομή της: την πιο τολμηρή και αδιανόητη περιπέτεια του ανθρώπινου πνεύματος». (Les fondements de mathématiques).
Στην ίδια κατηγορία ενδιαφερόντων βιβλίων που ασχολούνται με τα Μαθηματικά, αλλά με στοχασμούς για την Τέχνη, μπορεί να συμπεριληφθούν και τα εξής:
Alfred Rényi: Dialogues about Mathematics/ Διάλογοι για τα Μαθηματικά, Norbert Wiener: I’m a Mathematician, G. H. Hardy: A Mathematician’s Apology/ Η Απολογία ενός Μαθηματικού, και τα βιβλία του Henri Poincaré: Science and Hypothesis/ Επιστήμη και Υπόθεση, The Value of Science/ Η Αξία της Επιστήμης, Science and Method, και ο κατάλογος απέχει βέβαια πολύ από το να εξαντληθεί.
Αξιοσημείωτο ότι αυτοί οι συγγραφείς ασχολούνται με την ανάλυση της ομοιότητας μεταξύ Μαθηματικών και Τέχνης, στο επίπεδο της δημιουργίας και της αισθητικής αξίας. Ο Wiener παραδέχεται ότι, αντίθετα από τις ευρέως προσβάσιμες τέχνες -μουσική και ζωγραφική- τα Μαθηματικά, παρά τις πολλές ομοιότητες με αυτές τις τέχνες, είναι προσβάσιμα μόνο από ένα εξειδικευμένο τμήμα του κοινού. Αυτός, λοιπόν, καταλήγει στο συμπέρασμα: «Κάποιος, εκτός αν είναι μαθηματικός, δύσκολα δέχεται ότι τα Μαθηματικά έχουν μια πολιτισμική και αισθητική γοητεία, ότι αντιπροσωπεύουν κάτι που συνδέεται με την ομορφιά, τη δύναμη και την έμπνευση». Η ιδέα της αισθητικής αξίας των Μαθηματικών επισημαίνεται με τον ίδιο τρόπο από τον G. H. Hardy: «Τα παραδείγματα του μαθηματικού, όπως αυτά του ζωγράφου ή του ποιητή, πρέπει να μεταφέρουν την ιδέα της ομορφιάς. Οι ιδέες, τα χρώματα και οι λέξεις πρέπει να συναρμολογηθούν αρμονικά. Η ομορφιά είναι η πρώτη δοκιμασία: τα άσχημα Μαθηματικά δεν έχουν στέρεη θέση στον κόσμο». Ο ίδιος λέει επίσης: «ένας μαθηματικός, όπως ο ζωγράφος ή ο ποιητής, δημιουργεί πρότυπα. Αν τα πρότυπά του είναι πιο μόνιμα από τα δικά τους, αυτό συμβαίνει διότι αυτά είναι φτιαγμένα με ιδέες».
Στο Επιστήμη και Μεθοδολογία, ο Poincaré αποτίει φόρο τιμής στην ομορφιά των Μαθηματικών, την οποία τοποθετεί δίπλα στην ομορφιά των καλλιτεχνικών έργων: «Φαίνεται εκπληκτικό το γεγονός ότι η αισθαντικότητα πρέπει να συμπεριλαμβάνεται δίπλα-δίπλα σε μαθηματικές παρουσιάσεις που προφανώς απευθύνονται μόνο στη νοημοσύνη. Αλλά αυτό σημαίνει ότι ξεχνάμε την αίσθηση της μαθηματικής ομορφιάς, την αρμονία των αριθμών και των σχημάτων, την κομψότητα της Γεωμετρίας. Πρόκειται για ένα πραγματικό αισθητικό συναίσθημα που βιώνουν όλοι οι πραγματικοί μαθηματικοί. Η αισθαντικότητα είναι στην πραγματικότητα εδώ. Πρόσωπο με πρόσωπο με το δικό του έργο, ο γεωμέτρης ανακαλύπτει ένα είδος ευχαρίστησης παρόμοιας, και της ίδιας έκτασης, με εκείνη του καλλιτέχνη».
Είναι προφανές ότι όλοι αυτοί οι σπουδαίοι μαθηματικοί αναφέρονται σε ένα βαθιά ανθρωπιστικό τύπο Μαθηματικών, διασκορπίζοντας τον παραμορφωμένο χαρακτήρα της απάνθρωπης ψυχρότητας, που αποδίδεται στο μαθηματικό σύμπαν από ορισμένους σχολιαστές, οι οποίοι βρίσκονται σε πλήρη άγνοια. Πολλοί μαθηματικοί και λογικολόγοι έχουν ενδιαφερθεί να μελετήσουν τη φύση των μαθηματικών εννοιών και συλλογισμών. Με στόχο να βρει το μυστικό αυτού του τύπου επιχειρηματολογίας και κατά συνέπεια της μαθηματικής δημιουργίας, ο Γάλλος λογικολόγος Edmond Goblot εκθέτει το συμπέρασμά του στο Traité de Logique: «Το πνεύμα οδηγεί πράγματι τις δραστηριότητές του. Από όλες αυτές τις πράξεις, το πνεύμα επιλέγει ελεύθερα εκείνες που θεωρούνται κατάλληλες για τους σκοπούς του, και αυτή η ελευθερία δίνει το πλήρες πλαίσιο εφαρμογής σε μια οιονεί οριοθέτηση της λογικής εφεύρεσης. Αυτή η τέχνη είναι τόσο ελεύθερη όσο και δημιουργική, όπως αυτή του ζωγράφου, του μουσικού ή του ποιητή˙ κυριολεκτικά, είναι μια ποιητική τέχνη (poietike téhne)».
Στο Επιστήμη και Υπόθεση, ο Poincaré τονίζει την ίδια ιδέα της δημιουργικής ελευθερίας που καθορίζει τα Μαθηματικά. Αναλύοντας τον ρόλο των υποθέσεων/ αξιωμάτων που «περιορίζονται σε ορισμούς ή συγκεκαλυμμένες συμβάσεις», προσθέτει τα εξής: «Τα τελευταία βρίσκονται συχνά στα Μαθηματικά και τις παρακείμενες επιστήμες. Αυτές οι επιστήμες αποκομίζουν την αυστηρότητά τους ακριβώς από αυτή την πηγή˙ αυτός ο τύπος συμβάσεων είναι το αποτέλεσμα της ελεύθερης δραστηριότητας του πνεύματος, το οποίο στον τομέα αυτό είναι εντελώς απεριόριστο. Το πνεύμα είναι ελεύθερο να κάνει τους δικούς του ισχυρισμούς, επειδή κατέχει τη δύναμη να αποφασίσει». Η ίδια ενοποιητική λέξη εμφανίζεται στο θαυμαστικό του Abraham Fraenkel: «Ελευθερία! Αυτή η λέξη μόνο συνοψίζει την πράξη της δημιουργίας των σύγχρονων Μαθηματικών».
Τόσο τα Μαθηματικά όσο και η Ποίηση περιλαμβάνουν αυτό που ο Marcus ονομάζει ‘σημειωτική βελτιστοποίηση: το μέγιστο του νοήματος στο ελάχιστο της έκφρασης’. Η συμπίεση δεν είναι δυνατή και είναι δύσκολη μια συμπύκνωση ή σύνταξη μιας περίληψης ή περίληψης που διατηρεί την αρχική γεύση. Ο Marcus παρατηρεί επίσης την ‘αλληλεγγύη’ μεταξύ των «τοπικών και παγκόσμιων πτυχών/ απόψεων», με την οποία αναφέρεται στην ικανότητα της Ποίησης για μια απομονωμένη λέξη ή έκφραση, η οποία και να λαμβάνει και να δίνει νόημα στο σύνολο. Συγκρίνει αυτό με την αναλυτικότητα στα Μαθηματικά όπου η συμπεριφορά μιας αναλυτικής συνάρτησης σε μια τοπική περιοχή/ γειτονιά καθορίζει την ολική συμπεριφορά της. Είναι επίσης αλήθεια για τα Μαθηματικά ως ενιαίο σύνολο. Όπως παρατήρησε ο Marcus, ο τομέας της σημειωτικής, και ιδίως των Μαθηματικών και της μεταφοράς, είναι ιδιαίτερα πλούσιος που αξίζει περαιτέρω διερεύνηση. Αξίζει να αναφερθεί και η παράλληλη έκφραση του Jung ‘ψυχή είναι η μέγιστη ένταση στην ελάχιστη έκταση’.
Σύμφωνα με τον Τσέχο ποιητή και γιατρό Miroslav Holub, δεν υπάρχει κοινή γλώσσα και κοινό δίκτυο σχέσεων και αναφορών στην Ποίηση και τα Μαθηματικά. Η Ποίηση δεν είναι το πράγμα που ειπώθηκε, αλλά ένας τρόπος να το πούμε. Για τις επιστήμες, οι λέξεις είναι βοηθητικό εργαλείο. Στην ανάπτυξη της σύγχρονης Ποίησης οι λέξεις οι ίδιες μετατρέπονται σε αντικείμενα. Η βάση της Ποίησης είναι το ανείπωτο, ενώ η Επιστήμη πρέπει να πει τα πάντα. Σκοπός της επιστημονικής επικοινωνίας είναι να μεταδώσει σαφή πληροφορία σχετικά με μια πτυχή μιας συγκεκριμένης άποψης της πραγματικότητας. Σκοπός της ποιητικής επικοινωνίας είναι να εισαγάγει ένα συναφές συναίσθημα ή να πιαστεί από τη μία πτυχή της ανθρώπινης συνθήκης. Έχω επανειλημμένα εντυπωσιαστεί ακούγοντας από επιστήμονες συναδέλφους ότι διαβάζουν Ποίηση, γιατί είναι σύντομη, στιγμιαία και ανταμείβει αμέσως, όπως πρέπει να είναι και ένα καλό επιστημονικό άρθρο.
Από την άλλη, ο Joel Cohen ισχυρίζεται ότι η Ποίηση και τα Μαθηματικά συνδυάζουν ετερόκλητα πράγματα επιδιώκοντας να συνθέσουν πολλαπλές έννοιες και ομορφιά χρησιμοποιώντας σύμβολα. Αυτά τα σύμβολα δείχνουν προς πράγματα έξω από τον εαυτό τους και δημιουργούν εσωτερικές δομές που στοχεύουν στην ομορφιά. Λίγα σύμβολα με κατάλληλη χρήση μεταδίδουν πολλά νοήματα. Εκτός από τις έννοιες που μεταφέρονται με τυποποιημένα σύμβολα, η Ποίηση και τα Μαθηματικά έχουν κοινό την οικονομία και το μυστήριο. Οι διαφορές μεταξύ Ποίησης και Μαθηματικών συνυπάρχουν με κοινές στρατηγικές συμβολισμού εμπειριών. Η αναγνώριση αυτών των κοινών στοιχείων καθιστά την Ποίηση σημείο εισόδου στην κατανόηση της καρδιάς των Μαθηματικών και κάνει, αντίστοιχα, τα Μαθηματικά σημείο εισόδου στην κατανόηση της καρδιάς της Ποίησης. Με αυτή την κατανόηση, τόσο η Ποίηση όσο και τα Μαθηματικά γίνονται σημεία εισόδου στην κατανόηση των άλλων και του εαυτού μας ως όντα που δημιουργούν και χρησιμοποιούν σύμβολα.
Τέλος, με αφορμή την αναφορά στον Miroslav Holub, αξίζει η μνεία στη συλλογή δοκιμίων του Kurt Brown. Ο Brown (The Measured Word: On Poetry and Science) διαπιστώνει ότι, ενώ οι χρήσεις της γλώσσας του επιστήμονα και του ποιητή μερικές φορές δουλεύουν σε διασταυρούμενους/ ανταγωνιζόμενους σκοπούς, οι ιδιοσυγκρασίες τους και οι δημιουργικές διαδικασίες τους βρίσκονται σε πλήρη αντιστοιχία. Αυτό όμως για να γίνει κατανοητό απαιτείται εμπνευσμένη και διευρυμένη ανάγνωση και από τις δυο πλευρές του χάσματος. Δοκίμια για τη σχέση Επιστήμης και Ποίησης, των Alice Fulton, Forrest Gander, Miroslav Holub, Paul Lake, Alison Hawthorne Deming, Stephanie Strickland κ.ά., παρουσιάζουν ποικιλία απόψεων και στοχασμών σχετικά με τις ομοιότητες και διαφορές μεταξύ της ποιητικής και της επιστημονικής φαντασίας. Αυτό που έχουμε στο The Measured Word είναι ένα σύνολο ‘γεφυροποιών’ οι οποίοι έχουν επανασυνδέσει τους ξεχωριστούς κόσμους της Τέχνης και της Επιστήμης˙ και είναι ευχαρίστηση να στέκεσαι στη μέση αυτής της γέφυρας και να αγναντεύεις και από τις δύο πλευρές της θέας.
Πρόκειται για ανακαλυπτικά δοκίμια για την περίεργη σχέση -και συναρπαστική συζήτηση- μεταξύ Επιστήμης και Ποίησης. Αν και τα ενδιαφέροντα της Επιστήμης και της Τέχνης συχνά φαίνονται να βρίσκονται σε απέναντι πόλους, ο Brown συγκεντρώνει μια ανθολογία δοκιμίων που φωτίζουν τις ιστορικές -και εξελισσόμενες- σχέσεις μεταξύ της ποιητικής και της επιστημονικής φαντασίας. Συγκεντρώνοντας τα κείμενα κορυφαίων σύγχρονων ποιητών, δοκιμιογράφων και στοχαστών, ο Brown τονίζει τους τρόπους με τους οποίους οι ποιητές χρησιμοποιούν τα επιστημονικά ευρήματα και τις μαθηματικές ιδέες για την καλλιτεχνική τους έκφραση -και προσφέρει μια εικόνα για την πρόσφατη ενσωμάτωση της τεχνολογίας και άλλων ανακαλύψεων στη μεταμοντέρνα Ποίηση. Υπάρχουν στοχασμοί για τις ομοιότητες και διαφορές μεταξύ της ποιητικής και της επιστημονικής φαντασίας, για την ποιητική χρήση των φράκταλ, για το υπερκείμενο (hypertext), για το μεταβαλλόμενο σχήμα της Ποίησης στην επιστημονική εποχή. Αυτές οι απόψεις συμπληρώνονται από πολλές προσεγμένες και καινοτόμες παρουσιάσεις ποιητών ενημερωμένων για τις επιτεύξεις των επιστημών. Τα κείμενα της συλλογής αυτής όχι μόνο γιορτάζουν την εμφάνιση μιας νέας εποχής ανακάλυψης, αλλά και εντοπίζουν την αναγκαιότητα αναθεώρησης της δυτικής σκέψης που χωρίζει το μυαλό και την καρδιά, αντικαθιστώντας τη διαίρεση αυτή με την αμοιβαιότητα της αλληλεπιδραστικής επικοινωνίας.
Πηγές Πληροφορίας
Brescan, M. (2009). Mathematics and art. Scientific Studies and Research, Series Mathematics and Informatics 19(2), 99 – 118.
Bernard, J. (1981). Création poétique et création scientifique. Bulletin de l’Association Guillaume Budé 3, 275-283. Paris.
Brown, K. (ed.) (2001). The Measured Word: On Poetry and Science. University of Georgia Press, Athens, Georgia.
Cohen, J. (2011). Mixing Apples and Oranges: What Poetry and Applied Mathematics Have in Common. Proceedings of the American Philosophical Society 155 (June), 189–202.
Goblot, E. (1937). Traité de Logique. Armand Colin, Paris.
Gonseth, F. (1926/ 1974). Les Fondements des Mathématiques. De la Géométrie d’Euclide à la Relativité générale et à l’Intuitionisme. Librairie Scientifique et Technique Albert Blanchard, Paris, Broche.
Gonseth, F. (1936/ 1974). Les Mathématiques et la Réalité. Essai sur la méthode axiomatique. Librairie Scientifique et Technique Albert Blanchard, Paris, Broche.
Growney, J. (2008). Mathematics Influences Poetry. Journal of Mathematics and the Arts 2 (March), 1–7.
Hadamard, J. (1945/ 1954). The Psychology of Invention in the Mathematical Field. Princeton University Press/ Dover, NY.
Hadamard, J. (1995). Η Ψυχολογία της Επινόησης στα Μαθηματικά. Κάτοπτρο, Αθήνα.
Hardy, G. H. (1991). Η Απολογία ενός Μαθηματικού. Πανεπιστημιακές Εκδόσεις Κρήτης.
Hardy, G. H. (2012). A Mathematician’s Apology. Cambridge University Press; Reissue edition.
Holub, M. (2001). Poetry and Science: The Science of Poetry / The Poetry of Science. In The Measured Word: On Poetry and Science, edited by Kurt Brown. University of Georgia Press, Athens, Georgia.
Marcus, S. (1970). The Mathematical Poetics. Bucureşti, Academia.
Marcus, S. (1986). The Shock of Mathematics. Bucureşti, Albatros.
Marcus, S. (1986). Art and Science. Bucureşti, Eminescu.
Marcus, S. (1989). Invention and Discovery. Bucureşti, Cartea Românească.
Marcus, S. (1998). Linguistic and Semiotic Preliminaries to Contextual Grammars.
In Mathematical and Computational Analysis of Natural Language: Selected papers from the 2nd International Conference on Mathematical Linguistics (ICML ’96), Tarragona, 1996. Edited by Carlos Martín-Vide, Studies in Functional and Structural Linguistics 45.
Morse, M. (1959). Mathematics and the arts. In Science and art, Bulletin of the Atomic Scientists 15(2), February.
Poincaré, H. (1912). Επιστήμη και Υπόθεση. Φέξης, Αθήνα.
Poincaré, H. (1997). Η Αξία της Επιστήμης. Κάτοπτρο, Αθήνα.
Poincaré, H. (2019). Science and Method. Pantianos Classics.
Poincare, H. (Author), Stillwell, J. (Translator) (2000). Papers on Fuchsian Functions. Springer; 1985 edition. [The Poincaré Work on Fuchsian/ automorphic Functions].
Renyi, A. (1967). Dialogues on Mathematics. Holden Day Inc.
Renyi, A. (1979). Διάλογοι για τα Μαθηματικά. Διογένης, Αθήνα.
Tóth, I. (1969). Achilles. The Eleatic Paradoxes in the Phenomenology of the Spirit. Bucureşti, Ştiinţifică.
Whitehead, A. N. (1997). Science and the Modern World. Simon and Schuster.
Wiener, N. (1964). I Am a Mathematician. MIT Press.