Στο άρθρο αυτό παρουσιάζουμε Ανθολογίες Μαθηματικής Ποίησης και τις απόψεις των μαθηματικά καταρτισμένων συντακτών τους. 

Ερευνούμε πώς οι ποιητές βλέπουν τα Μαθηματικά και χρησιμοποιούν μαθηματικά στοιχεία και εικόνες στα ποιήματά τους. Δύο εξέχουσες προσωπικότητες στις ΗΠΑ είναι οι πανεπιστημιακοί μαθηματικοί και ποιήτριες Sarah Glaz και JoAnne Growney. Και οι δύο έχουν κάνει πολλά για να συνειδητοποιηθούν οι πιθανές συνδέσεις μεταξύ Μαθηματικών και Ποίησης και το 2008 συν-επιμελήθηκαν το Strange Attractors: Poems of Love and Mathematics, μια ποιητική ανθολογία που χρησιμοποιεί συγκεκριμένα μαθηματικά καλολογικά στοιχεία. Παρατηρώντας ότι τα μαθηματικά ποιήματα σπάνια εμφανίζονται σε κυρίαρχες λογοτεχνικές εκδόσεις, η επιλογή των Glaz και Growney χρονολογείται από τον βιβλικό Βασιλιά Σολομώντα και τον Κάτουλλο, μέχρι τις μέρες μας. Τα ποιήματα περιλαμβάνουν διάφορες αναφορές στα Μαθηματικά, σε περιεχόμενο, μορφή και εικόνες, που κυμαίνονται από την απλή μέτρηση έως κρυφές μαθηματικές νύξεις και προχωρημένη Άλγεβρα.

Οι Glaz και Growney περιγράφουν μια από τις πρώτες γνωστές ποιήτριες, από τη Σουμεριανή Μεσοποταμία, την Enheduanna, η οποία ήταν αρχιέρεια του θεού της σελήνης γύρω στο 2300 π.Χ. Η Enheduanna ήταν προστάτης των γραπτών τεχνών και των μαθηματικών υπολογισμών. Αυτά περιλάμβαναν αστρονομικούς ημερολογιακούς υπολογισμούς και Μαθηματικά που σχετίζονται με τη μηχανική και τη ρύθμιση ορίων ιδιοκτησίας: τα πρώιμα Μαθηματικά δεν περιλάμβαναν την περίπλοκη εξειδικευμένη εργασία που σχετίζεται με τα σύγχρονα Μαθηματικά. Αναφορικά με τον διαχωρισμό των Μαθηματικών και των τεχνών, οι Glaz και Growney το συνδέουν με τη γενική αύξηση της γνώσης, την εξειδίκευση και τον επακόλουθο διαχωρισμό των κλάδων που έλαβε χώρα στη σύγχρονη περίοδο, στον βαθμό που ο όγκος της διαθέσιμης γνώσης έχει ξεπεράσει τη μαθησιακή ικανότητα οποιουδήποτε ατόμου.

Οι Glaz και Growney εντοπίζουν μικρό αριθμό προσπαθειών για την αντιμετώπιση των Μαθηματικών στην Ποίηση πριν από τη δική τους ανθολογία, όπως το Memorabilia Mathematica του Robert Moritz το 1914, μια συλλογή ανέκδοτων, στίχων και αφορισμών που σχετίζονται με τα Μαθηματικά, που περιλαμβάνει και ποίηση των Dante, Goethe και Tennyson. Οι Glaz και Growney βρίσκουν ότι η παλαιότερη συλλογή ειδικά μαθηματικής Ποίησης χρονολογείται από το 1979, των Ernest Robson και Jet Wimp: Against Infinity – An Anthology of Contemporary Mathematical Poetry.

Το 2008 η Growney περιέγραψε διάφορους τομείς μαθηματικής επιρροής στην Ποίηση, σε ένα άρθρο που ξεκινά σημειώνοντας ομοιότητες μεταξύ των δύο: ότι η γλώσσα και των δύο ευνοεί ρητά την ακρίβεια και τη συνοπτική σαφήνεια, ότι κάθε λέξη και σύμβολο επιλέγεται με ιδιαίτερη προσοχή και ότι το νόημα προφανώς δημιουργείται από κάτι σχετικά μικρό στη σελίδα. Αναγνωρίζοντας ότι είναι δύσκολο να οριστεί κάποιος από τους δύο τομείς με ακρίβεια, υποστηρίζει ότι και οι δύο περιλαμβάνουν ωστόσο «γλώσσα», «φαντασία», «κομψότητα» και «απόλαυση». Αναφέρει τον ισχυρισμό του T. S. Eliot ότι η ποίηση «μπορεί να επικοινωνήσει πριν γίνει κατανοητή» και προτείνει ότι και τα Μαθηματικά μοιράζονται αυτό το χαρακτηριστικό. H Growney συνεχίζει συζητώντας τη σημασία της μέτρησης στην ποίηση, τις συλλαβές και τους στίχους, που είναι ένα ουσιαστικό χαρακτηριστικό.

Η Growney δεν προσπαθεί πάντα να προωθήσει κάποια θεωρία για το πώς μπορεί να σχετίζονται τα Μαθηματικά και η Ποίηση, προτιμώντας να προσφέρει τα ποιήματα ως έχουν, παρατηρώντας ότι η χρήση μαθηματικής ορολογίας και εικόνων δημιουργεί μια ιδιαίτερη παραστατικότητα. Υποδεικνύοντας ότι τέτοιες εικόνες διαφορετικά δεν θα μπορούσαν να αποδοθούν εύκολα στη συνηθισμένη γλώσσα, καταλήγει: Αυτοί οι ποιητές χρησιμοποιούν μαθηματικούς όρους για να μας δώσουν την εικόνα που αξίζει όσο χίλιες λέξεις. Αυτή η παρατήρηση περικλείει ένα σημαντικό σημείο: ότι τόσο τα Μαθηματικά όσο και η Ποίηση μοιράζονται μια συναισθηματική ιδιότητα, που αλλιώς δεν μπορεί να περιγραφεί.

Σε ένα παρόμοιο έργο του 2011, η Glaz συζητά διάφορα ποιήματα εμπνευσμένα από τα Μαθηματικά, που κυμαίνονται από το μέτρημα στην αρχαία Μεσοποταμία έως τις γεωμετρικές γωνίες στο «A Mathematical Problem» του Coleridge και ένα του Guillevic για τις παράλληλες γραμμές. Ο Eugène Guillevic (1907-1997) ήταν Γάλλος ποιητής, μια από τις συλλογές του οποίου, η Euclidiennes, είναι μια σειρά από μονοσέλιδα ποιήματα, το καθένα προλογίζεται από ένα απλό μαθηματικό σχήμα που προέρχεται από τα Στοιχεία του Ευκλείδη, όπως παράλληλες γραμμές, ένα σημείο ή ένα τρίγωνο, και στη συνέχεια μια απάντηση σε στίχο σε αυτή τη γεωμετρική εικόνα.

Η Glaz συνοψίζει εν συντομία τις βασικές έννοιες στα Μαθηματικά όπως η Άλγεβρα, ο Λογισμός, οι Σειρές, ο αριθμός e, η Θεωρία Συνόλων του Cantor, τα Θεμέλια των Μαθηματικών του Hilbert, το Θεώρημα της μη-πληρότητας του Gödel και τα σύνολα Mandelbrot, όλα όπως εμφανίζονται στα επιλεγμένα ποιήματα. Για παράδειγμα, το ποίημα της Sandra M. Gilbert, «He Explains the Book Proof» αναφέρεται στον Ούγγρο μαθηματικό Paul Erdős. Η Glaz καταλήγει στο συμπέρασμα ότι η «δύναμη της Ποίησης να προσελκύει την προσοχή και να ενισχύει τη μνήμη» είναι ένα εξαιρετικό εργαλείο για την εκπαίδευση στα Μαθηματικά, όπου οι ιδέες μπορούν να μεταφερθούν με αυτή τη μορφή.

 

Μια άλλη πρόσφατη ανθολογία μαθηματικής Ποίησης είναι η συλλογή του 2008 που επιμελήθηκε η μαθηματικός Marcia Birken και η θεωρητικός της λογοτεχνίας Anne Coon. Κάθε κεφάλαιο του βιβλίου τους παίρνει μια διαφορετική μαθηματική έννοια και αναλύουν λεπτομερώς την αναπαράστασή της στην Ποίηση, ξεκινώντας με μερικές από τις πιο στοιχειώδεις έννοιες όπως η μέτρηση και τα σχήματα, πριν προχωρήσουνε στη συμμετρία, τα φράκταλ και αυτά που περιγράφουν ως ‘μοτίβα του μυαλού’: απόδειξη, παράδοξο και άπειρο. Η κατηγοριοποίησή τους των διαφόρων εννοιών στα Μαθηματικά, καθώς σχετίζονται με την Ποίηση, είναι ενδιαφέρουσα.

Στην ενότητα τους για τη μέτρηση, οι Birken και Coon ξεκινούν με μια περιγραφή του τι είναι οι φυσικοί, οι ακέραιοι, οι πραγματικοί αριθμοί και ούτω καθεξής, και στη συνέχεια συζητούν τη μέτρηση στην Ποίηση -ρυθμό, αριθμό στίχων και μέτρηση σε στροφές. Στη συνέχεια μετρούν σε σχηματισμούς, όπως στο τρίγωνο του Pascal, την ακολουθία Fibonacci και τη χρυσή αναλογία, σε σύγκριση με τη μετρημένη μορφή και τις μεταθέσεις σε ποιητικά είδη όπως η σεστίνα, το σονέτο και η βιλανέλα. Τέλος, εξετάζουν τα σχήματα, ξεκινώντας με μαθηματικές περιγραφές επιπέδων, σπειρών και συμμετριών, προχωρούν δίνοντας παραδείγματα διαμορφωμένης Ποίησης και συμμετριών στη μορφή, με μια συζήτηση για την Υπερβολική Γεωμετρία, τη σχέση της με τον Escher και τη συμμετρία ως μεταφορά.

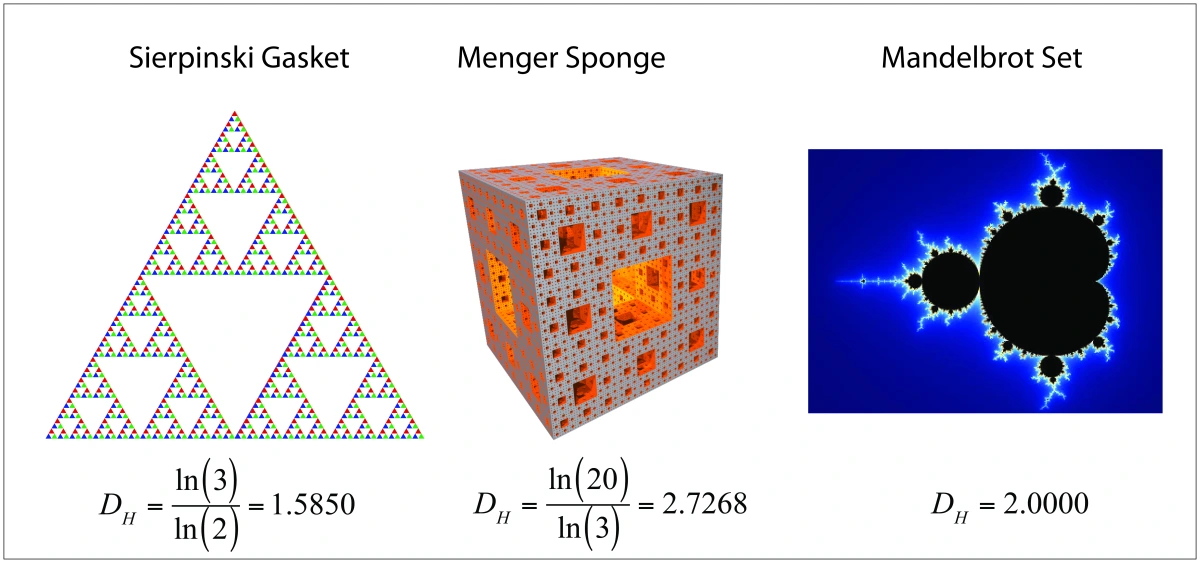
Τα φράκταλ είναι ένας άλλος τομέας των Μαθηματικών που συζητούν, ιδιαίτερα η αυτο-ομοιότητα, η αναδρομικότητα, η επανάληψη και η κλίμακα και η μεταφορά αυτών των χαρακτηριστικών σε συγκεκριμένα ποιήματα. Εντοπίζουν αυτά τα χαρακτηριστικά στη σύγχρονη Ποίηση εμπνευσμένη συνειδητά από τα Μαθηματικά, σημειώνοντας χαρακτηριστικά που μοιάζουν με φράκταλ σε ένα σονέτο του Σαίξπηρ και ένα γερμανικό ποίημα του 18ου αιώνα μοιάζει με τις λεγόμενες «παθολογικές» παράξενες καμπύλες των Hilbert και Peano.

Το ιδιαίτερο σημείο των Birken και Coon είναι ότι ενώ τα σύγχρονα Μαθηματικά έδωσαν τους τύπους και τις δημιουργημένες από υπολογιστή εικόνες φράκταλ (μια ανακάλυψη που ξεκίνησε από τον Mandelbrot), οι ίδιες οι έννοιες προϋπάρχουν στη φύση. Με άλλα λόγια, τα φράκταλ είναι ένα καλό παράδειγμα μιας όχι προφανώς μονοκατευθυντικής επιρροής από τα Μαθηματικά στην Ποίηση. Επιπλέον, υποστηρίζουν ότι η ποιητική ερμηνεία των φράκταλ προσθέτει στην διανοητική κατανόηση της έννοιας, επειδή είναι μια θεμελιωδώς ‘ποιητική’ έννοια. Παραθέτουν τον ίδιο τον Mandelbrot στο The Fractal Geometry of Nature: Η φύση των φράκταλ προορίζεται να ανακαλύπτεται σταδιακά από τον αναγνώστη, όχι να αποκαλύπτεται αστραπιαία από τον συγγραφέα.

Λαμβάνοντας υπόψη αυτό το πλαίσιο, το σχόλιο του Mandelbrot για τα Μαθηματικά είναι φυσικά άμεσα εφαρμόσιμο στην άσκηση της ποιητικής. Πράγματι, η Sarah Glaz έκανε ανασκόπηση του βιβλίου των Birken και Coon το 2010, σχολιάζοντας: Υπάρχει μια βαθιά σύνδεση μεταξύ των Μαθηματικών και της Ποίησης τέτοια που αψηφά όλες τις προσπάθειες να δοθεί πλήρης εξήγηση. Η Glaz συνεχίζει λέγοντας ότι τα τελευταία χρόνια έχουν γίνει αυξημένες προσπάθειες να εξηγηθεί ή να τονιστεί η σύνδεση και ότι ένα από τα δυνατά σημεία του βιβλίου των Birken και Coon είναι ότι τονίζει τις συνδέσεις «χωρίς να ελαχιστοποιεί τις διαφορές τους».

Κλείνουμε αυτό το κείμενο με ένα σχετικό ποίημα της μαθηματικού και ποιήτριας Emily Grosholz:

 

 

Emily Grosholz

 

Εγκώμιο στα Fractals

Παραλλαγές στην Εισαγωγή στο

«The Fractal Geometry of Nature» του Benoit Mandelbrot

 

Η Γεωμετρία του Ευκλείδη δεν μπορεί να περιγράψει,

ούτε του Απολλώνιου, το σχήμα των βουνών,

λακκούβες, σύννεφα, χερσονήσους ή δέντρα.

Τα σύννεφα ποτέ δεν είναι σφαίρες,

ούτε τα βουνά κώνοι, ούτε τα πεύκα˙

ο φλοιός δεν είναι λείος˙ και εκεί όπου η γη και η θάλασσα

τόσο διαφορετικά απλώνονται η μια προς την άλλη

και ελαφριά φιλιούνται, δεν είναι υπερβολή.

Σε σύγκριση με τα στοιχειώδη σχήματα του Ευκλείδη,

η Φύση, χαλαρώνοντας τα μαλλιά της, παρουσιάζει μοτίβα

(γλυκιά αταξία, επιπλέουσα, αχτένιστη)

όχι απλώς υψηλότερου βαθμού n

αλλά μάλλον εντελώς διαφορετικού

επιπέδου πολυπλοκότητας:

το πλήθος των αναλογιών μεταξύ των αποστάσεων

που την περιγράφουν είναι σχεδόν άπειρο.

Πώς θα μελετήσουμε τη μορφολογία

του άμορφου; Ο Mandelbrot

έλυσε το αίνιγμα με την ανακάλυψη των fractals,

μια οικογένεια από μορφές

τρελαμένες από την τυχαιότητα, οι κανονικότητές τους

είναι όλες στατιστικές, όπως η κίνηση Brown,

οι όμορφες διαμορφώσεις τους

αποδεικνύονται ίδιες σε κάθε κλίμακα.

Ορισμένα fractal σύνολα είναι καμπύλες

(καμπύλες πλήρωσης χώρου!) ή μιγαδικές επιφάνειες˙

άλλα είναι εντελώς αποκομμένες ‘σκόνες’˙

άλλα είναι πάρα πολύ παράξενα για να έχουν όνομα.

Ο Poincaré παρατήρησε κάποτε,

μπορεί να υπάρχουν ερωτήσεις που επιλέγουμε να ρωτήσουμε,

αλλά άλλοι αναρωτιούνται,

μερικές φορές για αιώνες, ενώ κανένας δεν ακούει.

 

 

Ερωτήσεις που ρωτούν τον εαυτό τους χωρίς ανάπαυση

μπορεί τελικά να αναπαυτούν στο μυαλό κάποιου.

Έτσι, ο Mandelbrot εγκαίρως

σχεδίασε την ομάδα των fractal του θαυμαστή

όχι μόνο για την κομψότητα της μορφής

ως μαθηματική δομή,

αλλά ως δύναμη να ερμηνεύει, σπείρα τη σπείρα,

το χτένισμα της Φύσης από μόρια και βουνά.

 

Τι ευγενής επανάσταση των ιδεών

διαχωρίζει τον δέκατο ένατο αιώνα από τον δικό μας!

Το σύνολο του Cantor από φωλιασμένα απόντα τρίτα,

η καμπύλη του Peano κλασματικής διάστασης,

τα fractals του Mandelbrot, αντιτίθενται στον παλιό κανόνα

της απλής συνέχειας,

εξημερώνοντας αυτό που κοντόφθαλμα

κάποτε θεωρήθηκε τερατώδες.

 

Η Φύση αγκαλιάζει τα τέρατα ως δικά της,

ενθαρρύνοντας τον σκεπτόμενο μαθηματικό

να βρει ανωμαλία

εγγενή στα πλάσματα γύρω μας.

Οι κύριοι του άπειρου,

Cantor, Peano, Hausdorff και Lebesque,

ανακάλυψαν σύνολα τελικά όχι υπερβατικά

αλλά έμφυτα, αγαπημένη Αιτία του Spinoza.

 

Η φαντασία πυροβολεί το αεράκι με τη Φύση,

και αυτό που λένε (Μαθηματικά) καθώς φλερτάρουν

αποκαλύπτεται εκπληκτικά αποτελεσματικό

στην επιστήμη, ένα δουλεμένο δώρο

που δεν αξίζουμε ή αναζητούμε ή καταλαβαίνουμε.

Ας είμαστε λοιπόν ευγνώμονες,

και να ελπίζουμε ότι θα συνεχιστεί, αν και η χαρά μας

πάντα εξισορροπείται από τη σύγχυσή μας.