Στην προηγούμενη ανάρτηση της 18ης Ιουλίου αναφέρθηκα στην ‘Ποίηση που εμπνέεται από τα Μαθηματικά’ και με συγκεκριμένο θέμα τα λεγόμενα Θεμέλια των Μαθηματικών. Στο άρθρο αυτό παρουσιάζονται ποιήματα εμπνευσμένα από τα Σύγχρονα Μαθηματικά.
-
Τα Fractals και ο Mandelbrot
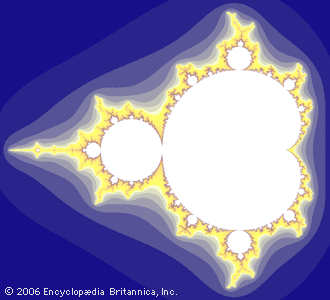
Είναι ευκολότερο να αποκτήσουμε άποψη για προηγούμενα μαθηματικά επιτεύγματα, παρά να χαρακτηρίσουμε το μαθηματικό τοπίο του παρόντος. Παρ’ όλα αυτά, είναι δυνατόν να επισημανθούν αρκετά σύγχρονα μαθηματικά αποτελέσματα που είχαν αντίκτυπο στον πολιτισμό. Πάνω από όλα είναι η Γεωμετρία των φράκταλ (fractal geometry), η οποία αναπτύχθηκε από τον Benoit Mandelbrot (1924-2010) το 1970. Σε λιγότερο από 40 χρόνια η Γεωμετρία αυτή έχει τόσο παγιωθεί στην κουλτούρα που δεν χρειάζεται εισαγωγή -η εικόνα του συνόλου Mandelbrot (Εικόνα *) είναι άμεσα αναγνωρίσιμη από κάθε καλλιεργημένο άνθρωπο. Μπορούμε να σκεφτούμε αν η έλξη που ασκεί η Γεωμετρία των φράκταλ έγκειται στην ομορφιά των εικόνων της, που παράγονται από Η/Υ, ή στη δύναμή της να περιγράψει την φαινομενικά τυχαία και χαοτική τάξη του κόσμου. Όποια και αν είναι η εξήγηση, η Γεωμετρία των φράκταλ πρωταγωνιστεί σε πολλά ποιήματα. Το παρακάτω απόσπασμα προέρχεται από ένα τραγούδι που συνέθεσε ο αμερικανός ποιητής, λαϊκός τραγουδιστής και συγγραφέας Jonathan Coulton.
Σύνολο Mandelbrot
Παθολογικά τέρατα! φώναξε ο τρομαγμένος μαθηματικός
Καθένα από αυτά είναι θραύσμα στο μάτι μου
Μισώ τον Χώρο Peano και την Καμπύλη Koch
Φοβάμαι το Σύνολο Cantor
Και το Τρίγωνο Sierpinski με κάνει να θέλω να κλάψω
Και ένα εκατομμύριο μίλια μακριά μια πεταλούδα φτερούγισε
Mια κρύα μέρα του Νοέμβρη γεννήθηκε ένας άνθρωπος ονόματι Benoit Mandelbrot
Η περιφρόνησή του για τα καθαρά Μαθηματικά και οι μοναδικές γεωμετρικές του ενοράσεις
Τον εξόπλισαν γερά να αντιμετωπίσει αυτούς τους δαίμονες
Είδε ότι η απεριόριστη πολυπλοκότητα μπορεί να περιγραφεί με απλούς κανόνες
Χρησιμοποίησε τον γιγαντιαίο του εγκέφαλο για να γυρίσει το παιχνίδι
Και κοίταξε κάτω από τη θύελλα και είδε ένα όραμα μέσα στο κεφάλι του
Μια βολβώδη αγκαθωτή μορφή
Πήρε το μολύβι του και κατέγραψε το μυστικό του
……………………
Πάρτε ένα σημείο Z στο μιγαδικό επίπεδο
Ας είναι το Z1 το τετράγωνο του Ζ συν C
Και το Ζ2 είναι το τετράγωνο του Ζ1 συν C
Και το Z3 είναι το τετράγωνο του Z2 συν C και ούτω καθεξής
Αν η σειρά των Z πρέπει πάντα να παραμείνει
Κοντά στο Z και ποτέ δεν φεύγει μακριά
Αυτό το σημείο ανήκει στο Σύνολο Mandelbrot
Σύνολο Mandelbrot είσαι ένα Test Rorschach στη φωτιά
Είσαι χρυσίζων πτεροδάκτυλος
Είσαι καρδιόσχημο κουτί από ελατήρια και σύρμα
Είσαι ένα κακό γαμημένο φράκταλ
Και είσαι ακριβώς στην ώρα να σώσεις τη μέρα
Διώχνοντας όλους τους φόβους μας μακριά
Μπορείς να αλλάξεις τον κόσμο με λεπτό τρόπο.
Υπάρχει επίσης το ποίημα της Emily Grosholz:
Εγκώμιο στα Fractals
Η Γεωμετρία του Ευκλείδη δεν μπορεί να περιγράψει,
ούτε του Απολλώνιου, το σχήμα των βουνών,
λακκούβες, σύννεφα, χερσονήσους ή δέντρα.
Τα σύννεφα ποτέ δεν είναι σφαίρες,
ούτε τα βουνά κώνοι, ούτε τα πεύκα˙
ο φλοιός δεν είναι λείος˙ και εκεί όπου η γη και η θάλασσα
τόσο διαφορετικά απλώνονται η μια προς την άλλη
και ελαφριά φιλιούνται, δεν είναι υπερβολή.
Σε σύγκριση με τα στοιχειώδη σχήματα του Ευκλείδη,
η Φύση, χαλαρώνοντας τα μαλλιά της, παρουσιάζει μοτίβα
(γλυκιά αταξία, επιπλέουσα, αχτένιστη)
όχι απλώς υψηλότερου βαθμού n
αλλά μάλλον εντελώς διαφορετικού
επιπέδου πολυπλοκότητας:
το πλήθος των αναλογιών μεταξύ των αποστάσεων
που την περιγράφουν είναι σχεδόν άπειρο.
Πώς θα μελετήσουμε τη μορφολογία
του άμορφου; Ο Mandelbrot
έλυσε το αίνιγμα με την ανακάλυψη των fractals,
μια οικογένεια από μορφές
τρελαμένες από την τυχαιότητα, οι κανονικότητές τους
είναι όλες στατιστικές, όπως η κίνηση Brown,
οι όμορφες διαμορφώσεις τους
αποδεικνύονται ίδιες σε κάθε κλίμακα.
Ορισμένα fractal σύνολα είναι καμπύλες
(καμπύλες πλήρωσης χώρου!) ή μιγαδικές επιφάνειες˙
άλλα είναι εντελώς αποκομμένες ‘σκόνες’˙
άλλα είναι πάρα πολύ παράξενα για να έχουν όνομα.
Ο Poincaré παρατήρησε κάποτε,
μπορεί να υπάρχουν ερωτήσεις που επιλέγουμε να ρωτήσουμε,
αλλά άλλοι αναρωτιούνται,
μερικές φορές για αιώνες, ενώ κανένας δεν ακούει.
Ερωτήσεις που ρωτούν τον εαυτό τους χωρίς ανάπαυση
μπορεί τελικά να αναπαυτούν στο μυαλό κάποιου.
Έτσι, ο Mandelbrot εγκαίρως
σχεδίασε την ομάδα των fractal του
θαυμαστή όχι μόνο για την κομψότητα της μορφής
ως μαθηματική δομή,
αλλά ως δύναμη να ερμηνεύει, σπείρα τη σπείρα,
το χτένισμα της Φύσης από μόρια και βουνά.
Τι ευγενής επανάσταση των ιδεών
διαχωρίζει τον δέκατο ένατο αιώνα από τον δικό μας!
Το σύνολο του Cantor από φωλιασμένα απόντα τρίτα,
η καμπύλη του Peano κλασματικής διάστασης,
τα fractals του Mandelbrot, αντιτίθενται στον παλιό κανόνα
της απλής συνέχειας,
εξημερώνοντας αυτό που κοντόφθαλμα
κάποτε θεωρήθηκε τερατώδες.
Η Φύση αγκαλιάζει τα τέρατα ως δικά της,
ενθαρρύνοντας τον σκεπτόμενο μαθηματικό
να βρει ανωμαλία
εγγενή στα πλάσματα γύρω μας.
Οι κύριοι του άπειρου,
Cantor, Peano, Hausdorff και Lebesque,
ανακάλυψαν σύνολα τελικά όχι υπερβατικά
αλλά έμφυτα, αγαπημένη Αιτία του Spinoza.
Η φαντασία πυροβολεί το αεράκι με τη Φύση,
και αυτό που λένε (Μαθηματικά) καθώς φλερτάρουν
αποκαλύπτεται εκπληκτικά αποτελεσματικό
στην επιστήμη, ένα δουλεμένο δώρο
που δεν αξίζουμε ή αναζητούμε ή καταλαβαίνουμε.
Ας είμαστε λοιπόν ευγνώμονες,
και να ελπίζουμε ότι θα συνεχιστεί, αν και η χαρά μας
πάντα εξισορροπείται από τη σύγχυσή μας.
-
Η Σκόνη του Cantor
Το ποίημα του Rodrigo Siqueira, ‘The Cantor Dust’, του οποίου η εικόνα αναπαράγεται παρακάτω, είναι ένα διαφορετικό παράδειγμα της ‘φράκταλ ποίησης’ (fractal poetry). Χρησιμοποιεί την οπτική δομή του Συνόλου Cantor για να στείλει ένα ποιητικό και μαθηματικό μήνυμα. Το σύνολο Cantor κατασκευάζεται με την επανειλημμένη διαγραφή του μεσαίου τρίτου από κάθε διάστημα μιας αυξανόμενης συλλογής διαστημάτων. Η κατασκευή αρχίζει με τη διαγραφή του μεσαίου τρίτου από το διάστημα [0,1]. Στη συνέχεια, το μεσαίο τρίτο από κάθε ένα από τα δύο εναπομείναντα διαστήματα διαγράφεται. Στη συνέχεια ακολουθεί η διαγραφή του μεσαίου τρίτου από κάθε ένα από τα τέσσερα εναπομένοντα διαστήματα, και ούτω καθεξής. Η διαδικασία δεν τελειώνει ποτέ.
Ενώ η πρώτη γραμμή του ποιήματος μας καλεί να σκεφτούμε τι βρίσκεται μέσα στα δυναμικά συστήματα, η μορφή της υποδηλώνει το πρότυπο του φράκταλ ‘Cantor Dust’ -όπως φαίνεται στο Σχήμα. Εάν αυτό το ποίημα συνεχιζότανε σε μια άλλη γραμμή στο επόμενο επίπεδο επανάληψης, οι λέξεις θεωρητικά θα γίνονταν ακόμη μικρότερες και πιο αποσπασματικές, καθώς ένα μέρος των χαρακτήρων θα αφαιρείτο και πάλι. Αν και ο ποιητής δεν αφαιρεί ακριβώς το ένα τρίτο κάθε γραμμής, όπως συμβαίνει κατά τη δημιουργία του φράκταλ ‘Cantor Dust’, η συνεχής αφαίρεση περίπου του ενός τρίτου των χαρακτήρων σε κάθε επόμενη γραμμή μιμείται τη διαδικασία που χρησιμοποιήθηκε για τη δημιουργία του φράκταλ. Τι θα συμβεί αν το ποίημα συνεχιστεί; Οι λέξεις θα αποσυντεθούν;
Η αναπαράσταση του ποιήματος από το φράκταλ μας προκαλεί να εξετάσουμε το ενδεχόμενο να υπάρχουν περισσότερες γραμμές, αόρατες, που υπάρχουν μόνο στη φαντασία του αναγνώστη. Ο Siqueira έχει ενώσει τις οπτικές και θεωρητικές ιδιότητες του προτύπου ‘Cantor Dust’ σε ένα ποίημα του οποίου η μορφή και το περιεχόμενο αναφέρονται στα φράκταλ. Εκτός από τα ποιήματα όπου η φυσική διάταξη των λέξεων στη σελίδα υποδηλώνει ένα φράκταλ σχήμα, υπάρχουν πολλές περιπτώσεις όπου οι ποιητές αποκαλύπτουν γνώση των φράκταλ στη γλώσσα που χρησιμοποιούν. Αυτή η χρήση των φράκταλ μπορεί να είναι μεταφορική ή μπορεί να επεκταθεί στη δομή του ίδιου του ποιήματος, όταν ένας ποιητής χρησιμοποιεί πρότυπα φρασεολογίας που μπορούν να περιγραφούν ως φράκταλ.
-
Άλλα Θέματα από τα Σύγχρονα Μαθηματικά
Αρκετά σύγχρονα ορόσημα στα Μαθηματικά περιστρέφονται γύρω από τις μεγάλες εικασίες. Το 1996 ο Andrew Wiles απόδειξε το Τελευταίο Θεώρημα του Fermat (Fermat’s Last Theorem), το οποίο δηλώνει ότι οι εξισώσεις xn+yn= zn δεν έχουν θετικές ακέραιες λύσεις για το n μεγαλύτερο από 2. Το θεώρημα δηλώθηκε από τον Pierre de Fermat (1601-1665) στο περιθώριο του βιβλίου του Διόφαντου Αριθμητικά, συνοδευόμενο από τις λέξεις:« Έχω ανακαλύψει μια πραγματικά αξιοσημείωτη απόδειξη που το περιθώριο αυτό είναι πολύ μικρό για να την περιλάβει». Η αναζήτηση 350 χρόνων για μια λύση και το σημαντικό σώμα των Μαθηματικών που δημιουργήθηκε στη διαδικασία κατέστησαν την απόδειξη του Wiles ένα από τα πιο αξιοσημείωτα μαθηματικά αποτελέσματα του αιώνα. Όπως αναμενόταν, αυτό το γεγονός γιορτάστηκε με ποιήματα, τα περισσότερα από τα οποία είναι χιουμοριστικά -είδος πολύ αγαπημένο από τους μαθηματικούς. Παρακάτω, ως μικρό δείγμα, είναι ένα χιουμοριστικό ποιηματάκι του Ted Munger από την ποιητική πρόκληση από το Τελευταίο Θεώρημα του Fermat.
Με Ακέραιο Μεγαλύτερο από 2
Με ακέραιο μεγαλύτερο από 2
Είναι κάτι που απλά δεν μπορείς να κάνεις.
Αν αυτό το περιθώριο ήταν πλατύ,
Θα σας τα έδειχνα όλα αυτά,
Αλλά δεν είναι, έτσι η απόδειξη αφήνεται σε σας!
Το Ινστιτούτο Μαθηματικών Clay, απαρίθμησε τα επτά πιο σημαντικά ανοικτά προβλήματα στα Μαθηματικά, τα Millennium Prize Problems. Ένα από τα προβλήματα της χιλιετίας, η υπόθεση Riemann, που προτάθηκε από τον Bernhard Riemann (1826-1866), γιόρτασε την εκατοστή πεντηκοστή επέτειό του το 2010. Η Υπόθεση Riemann είναι μια εικασία για τα μηδενικά της συνάρτησης zeta(s) ή ζ(s) του Riemann. Θεωρείται ότι είναι το πιο σημαντικό ανοιχτό πρόβλημα στα καθαρά Μαθηματικά, η λύση του οποίου θα προωθήσει τη γνώση μας για την κατανομή των πρώτων αριθμών. Παρακάτω είναι οι στίχοι του ελληνο-αμερικάνου σπουδαίου μαθηματικού Tom Apostol για την Υπόθεση του Riemann.
Πού Είναι τα Μηδενικά της Zeta του s;
(Μπορεί να τραγουδηθεί όπως το ‘Sweet Betsy from Pike’)
Πού είναι τα μηδενικά της zeta του s;
Ο Riemann έχει κάνει μια καλή εικασία˙
Είναι όλα στην κρίσιμη γραμμή, λέει ο ίδιος,
Και η πυκνότητα τους είναι πάνω από 2pi log t.
Αυτή η δήλωση του Riemann είναι σαν σκανδάλη
Και πολλοί καλοί άντρες, με σφρίγος και σθένος,
Έχουν προσπαθήσει να βρουν, με μαθηματική αυστηρότητα,
Τι συμβαίνει με τη zeta καθώς το mod t αυξάνει.
Οι προσπάθειες των Landau και Bohr και Cramer,
Και Littlewood, Hardy και Titchmarsh είναι εκεί,
Παρά τις προσπάθειές τους, την επιδεξιότητα και τη φινέτσα τους,
Στο να εντοπίσουν τα μηδενικά, υπήρξε ελάχιστη επιτυχία.
Το 1914 ο G.H. Hardy το βρήκε,
Ένας άπειρος αριθμός που βρισκόταν στη γραμμή,
Ωστόσο, το θεώρημά του δεν αποκλείει την περίπτωση,
Ότι μπορεί να υπάρχει μηδέν σε κάποιο άλλο μέρος.
Έστω P η συνάρτηση pi μείον li,
Η τάξη της Ρ δεν είναι γνωστή για μεγάλο x,
Εάν μπορούσαμε να δείξουμε την τετραγωνική ρίζα του x επί log x,
Τότε η εικασία του Riemann θα ήταν σίγουρα έτσι.
Σχετικά με αυτό είναι ένα άλλο αίνιγμα,
Θεωρώντας τη συνάρτηση Lindelof mu(sigma)
Η οποία μετρά την αύξηση στην κρίσιμη γραμμή,
του αριθμού των μηδενικών, μας δίνει μια λαβή.
Αλλά κανείς δεν ξέρει πώς συμπεριφέρεται αυτή η συνάρτηση,
Η κυρτότητα μας λέει ότι δεν μπορεί να έχει κυμάνσεις,
Ο Lindelof είπε ότι το σχήμα του γραφήματός του,
Είναι σταθερό όταν το σίγμα είναι μεγαλύτερο από το μισό.
Ω, πού είναι τα μηδενικά της zeta του s;
Πρέπει να γνωρίζουμε ακριβώς, δεν μπορούμε απλώς να μαντέψουμε,
Προκειμένου να ενισχυθεί το θεώρημα των πρώτων αριθμών,
Η καμπύλη του ολοκληρώματος δεν πρέπει να τους πλησιάζει πολύ.
Αρκετά άλλα ποιήματα έλκουν την έμπνευσή τους από τα millennium prize problems. Το 2004, στον Grigory Perelman προσφέρθηκε το Fields Medal για την επίλυση της Εικασίας Poincare. Αρνήθηκε να δεχτεί το βραβείο. Το ποίημα της JoAnne Growney, ‘Ο Perelman και Εγώ’ (Perelman and Me), συλλαμβάνει τα πολύπλοκα συναισθήματα που προκαλεί αυτή η άρνηση. Η μούσα της ποίησης ήταν όμως σιωπηλή όταν το 2010 ο Perelman απέρριψε το Clay Millennium Prize ύψους 1 εκατομμυρίου δολαρίων για την επίλυση της Εικασίας Poincare.
Ο Perelman και Εγώ
Την Τρίτη 22 Αυγούστου 2006 ο Ρώσος μαθηματικός Grigory Perelman απέρριψε το Fields Medal για τη συμβολή του, το 2004, στην απόδειξη μιας πολύ γνωστής και δύσκολης εικασίας, που είχε θέσει αρχικά ο Henri Poincaré. Επικροτώ την απομόνωση του Perelman.
Η βαρύτητα του σύμπαντος
απαιτεί σκοτεινή ύλη.
Επιλέγοντας μια σκέψη
αποτρέπεις μιαν άλλη.
Κοριτσάκια μαθαίνουν κοινωνικές χάρες
να κάνουν τους άλλους να αισθάνονται άνετα.
Αλλά οι φιλικοί χαιρετισμοί
δεν είναι ποτέ Μαθηματικά.
Οι δύσκολες σκέψεις
γεννιούνται σε απομόνωση:
η μεγαλοφυΐα γλιστρά μακριά εάν κοινωνικοποιηθεί-
έτσι πρέπει να αρνηθεί το βραβείο.
Ένα ποίημα του Haipeng Guo, ‘When a P–man Loves an NP–woman’, περιλαμβάνει το ακόμα άλυτο πρόβλημα, P vs. NP. Σε αυτό το ποίημα, η NP-γυναίκα ζητά από τον P-άντρα να λύσει την Εικασία ως προϋπόθεση για να τον παντρευτεί. Το Πρόβλημα P vs. NP είναι σημαντικό ανοικτό πρόβλημα στην επιστήμη των υπολογιστών. Το ερώτημα που θέτει είναι, εάν κάθε πρόβλημα, του οποίου η ύπαρξη λύσης μπορεί να επιβεβαιωθεί γρήγορα από έναν υπολογιστή, μπορεί επίσης και να επιλυθεί γρήγορα από τον υπολογιστή. Θεωρείται από πολλούς ως το πιο σημαντικό ανοικτό πρόβλημα στον τομέα αυτό. Πρόκειται για ένα από τα επτά προβλήματα του Millennium Prize από το Clay Mathematics Institute με αμοιβή 1 εκατομμύριο δολάρια. Ο όρος γρήγορα, που χρησιμοποιήθηκε παραπάνω, δηλώνει την ύπαρξη ενός αλγορίθμου για μια διαδικασία η οποία τρέχει σε πολυωνυμικό χρόνο. Η γενική κλάση ερωτημάτων για τα οποία κάποιος αλγόριθμος δίνει την απάντηση σε πολυωνυμικό χρόνο ονομάζεται P. Για κάποια ερωτήματα δεν υπάρχει γνωστός τρόπος για την γρήγορη εύρεση απάντησης, αλλά αν κάποιος διαθέτει πληροφορία που να αποδεικνύει ποια είναι η απάντηση, είναι δυνατό να επιβεβαιώσει την απάντηση γρήγορα. Η κλάση των προβλημάτων που μπορούν να ‘επιβεβαιωθούν’ σε πολυωνυμικό χρόνο ονομάζεται κλάση NP.
Όταν ένας Ρ-άντρας αγαπάει μια ΝΡ-γυναίκα
(Κατά μίμηση του γνωστού τραγουδιού When a man Loves a woman)
Ήμουν ένας ευτυχισμένος ντετερμινιστής άντρας
Με απλό πολυωνυμικό εγκέφαλο
Ευχαριστημένος με προβλήματα της P,
Και πάντα κοίταζα την NP με περιφρόνηση.
Αγάπησα μια πολυωνυμική γυναίκα,
Αλλά με μη ντετερμινιστικό πνεύμα,
Είπε ότι θα με παντρευτεί,
Μόνο αν μπορούσα να της αποδείξω ότι P = NP.
Έσπευσα στη βιβλιοθήκη και μελέτησα,
Ρώτησα τους Garey & Johnson* για μια υπόδειξη προς την αλήθεια,
Είπαν ‘είναι πολύ δύσκολη ερώτηση’,
Αλλά κανένας τους δεν είχε ιδέα ή ένδειξη.
Πήγα στην εκκλησία και προσευχήθηκα στον Παντοδύναμο,
«Παρακαλώ Κύριε, δώσε μου καθοδήγηση προς την αλήθεια»,
«Μη χάνεις τον καιρό σου γιέ μου», είπε γελώντας μια φωνή,
Γιατί εγώ ο ίδιος σε αυτό ξόδεψα τα νιάτα μου.
Ο πρώτος χρησμός λέει ότι θα παντρευτείτε
Ο δεύτερος ότι θα χωρίσετε
Ο χρόνος ρέει, οι διαδρομές διακλαδώνονται, τα αποτελέσματα μπορεί να διαφέρουν
Αποδεχτείτε την κατάσταση που τελικά ταιριάζει.
Αν τελικά παντρευτείς αυτό το κορίτσι,
Και P = NP ήταν αλήθεια,
Τι χάος: το e-banking ανασφαλές, Οι πωλητές ταξιδεύουν τζάμπα!
Και οι μαθηματικοί δεν έχουν τίποτα να κάνουν!
Αν σας δώσω την ευτυχία,
Η προϋπόθεση πρέπει να είναι όχι μάρτυρες,
Ακόμα αν και οι δύο δεν κάνατε τίποτα εντελώς λάθος,
Οι ποινές θα είναι εκθετικά μεγάλες.
Αν πραγματικά θέλεις να παντρευτείς αυτή τη γυναίκα,
Τότε η τυχαιότητα μπορεί να είναι το μόνο κλειδί,
Αλλά παρακαλώ σταμάτησε να προσεύχεσαι σε μένα για μια απάντηση,
Γιατί δεν μπορούσα να αποφασίσω για αυτό το P = NP!
* Αναφορά στο βιβλίο των Garey & Johnson: Computers and Intractability: A Guide to the Theory of NP-Completeness.
-
Επιλεγόμενα
Επανήλθα λοιπόν σύντομα, όπως είχα απειλήσει, με έννοιες και κατασκευές από τα σύγχρονα Μαθηματικά, γιατί υπάρχουν εν προκειμένω θέματα που εμπνέουν τους ποιητές, αλλά και τους ίδιους τους μαθηματικούς. Έννοιες όπως
τα Fractals του Mandelbrot, η Σκόνη του Cantor, το Τελευταίο Θεώρημα του Fermat,
η Υπόθεση Riemann, η Εικασία του Poincare, το πρόβλημα P vs. NP, περιλαμβάνονται σε αυτές που εμπνέουν ποιήματα και συνεπώς συνάδουν με αυτό που λέγεται ‘Ποίηση που εμπνέεται από τα Μαθηματικά’. Οφείλω πάντως να ομολογήσω ότι για να κατανοήσει κάποιος σε βάθος αυτού του είδους την ποίηση χρειάζεται να γνωρίζει και λίγα στοιχεία από τα σύγχρονα Μαθηματικά.
Πηγές Πληροφορίας
Glaz, S. (2011). Poetry inspired by mathematics: a brief journey through history. Journal of Mathematics and the Arts, 5(4), 171–183. [Όπου και εκτενής βιβλιογραφία].
Apostol, T. M. (2000). Where Are the Zeros of Zeta of s?, Historia Mathematica Mailing List Archives: Lyrics and Mathematics. http://www.sunsite.utk.edu/ math_archives/.http/hypermail/historia/dec99/0157.html.
Chapman, R. and Sprott, J. C. (2005). Images of a Complex World: The Art and Poetry of Chaos. World Scientific, London-Hackensack, NJ.
Coulton, J. Mandelbrot Set. http://www.jonathan coulton.com/songdetails/Mandelbrot%20Set/Links#.
Glaz, S. (2002). Calculus. Humanistic Math. Network. J. 26, p. 30.
Glaz, S. (2010). The enigmatic number e: A history in verse and its uses in the mathematics classroom. MAA Loci: Convergence, April. http://mathdl.maa.org/mathDL/46/?pa¼content&sa¼viewDocument&nodeId¼3482. MAA, Washington DC.
Glaz, S. (2010). Poetry inspired by mathematics. Proceedings of Bridges Pe´cs: Mathematics, Music, Art, Architecture, Culture. R. Sarhangi and G. Hart (eds.), Tessellations Publishing, Phoenix, AZ, pp. 35–43.
Glaz, S. and Growney, J. (eds.) (2008). Strange Attractors: Poems of Love and Mathematics. A K Peters, Wellesley, MA.
Grosholz, E. (1984). The River Painter. University of Illinois Press, Urbana-Champaign, IL.
Growney, J. (2006). Perelman and Me. MAA Focus 26(8), p. 7.
Growney, J. Intersections – poetry with mathematics. http://www.poetrywithmathematics.blogspot.com/.
Siqueira, R. The Cantor Dust. http://www.insite.com.br/ rodrigo/misc/fractal/fractal_poetry.html.
Teitelbaum, J. Fermat’s last theorem poetry challenge. http://www.math.uic.edu/jeremy/poetry.html.