Μια φορά κι έναν καιρό, όταν ήμουν παιδί, ανακάλυψα στην πλούσια βιβλιοθήκη του φιλόλογου πατέρα μου το παλιό βιβλίο του Γιάννη Σαραλή Νεοελληνική Μετρική, που είχε κυκλοφορήσει το 1939. Ανάμεσα στα άλλα ασχολείται και με τα στιχουργικά είδη με σταθερή μορφή και ως ένατο στη σειρά -μετά το σονέτο, τη μπαλάντα κτλ.- αναφέρει τη ‘Βιλλανέλλα’ (Villanelle). Μου άρεσε το όνομα, είχα και μια φίλη που την έλεγαν Νέλα και της κόλλησα το παρατσούκλι Νέλα – Βιλανέλα, κι έτσι μου ’μεινε να το θυμάμαι (μνημονοτεχνικός κανόνας). Αργότερα, όταν βρισκόμουν για σπουδές στο Reading, ανακάλυψα τη βιλανέλα του Auden. Δεκαετίες μετά, και στο πλαίσιο της έρευνας ‘Ποίηση και Μαθηματικά’, ανακάλυψα ένα σύντομο άρθρο των Grosholz & Glaz που αναφέρεται και στη βιλανέλα από μαθηματική πλευρά –αλλά ας πάρουμε τα πράγματα με τη σειρά.
-
Τι Είναι η Βιλανέλα
Η βιλανέλα αποτελεί πρότυπο ποιήματος που αρχικά παρουσιάζει σημαντική ποικιλία ως προς τον αριθμό των στροφών και το είδος της ομοιοκαταληξίας. Τελικά, όμως, επικρατούν μόνο δύο μορφές, αυτές των 19 και 13 στίχων αντίστοιχα και κυρίως η πρώτη. Αυτή αποτελείται από έξι (6) στροφές, από τις οποίες οι πρώτες πέντε (5) είναι τρίστιχες (3), με τύπο ομοιοκαταληξίας α – β – α, ενώ η τελευταία (1) είναι τετράστιχη (4) στροφή, με τύπο ομοιοκαταληξίας α – β – α – α. Έτσι έχουμε 5x3=15 και 1x4=4, σύνολο 19 στίχους, ενώ έχουμε μόνο δύο τύπους ομοιοκαταληξίας.
Επιπλέον, ο πρώτος στίχος της πρώτης στροφής επαναλαμβάνεται ως τρίτος της δεύτερης και της τέταρτης, και ο τρίτος στίχος πάλι της πρώτης στροφής επαναλαμβάνεται ως τρίτος της τρίτης και της πέμπτης. Αυτό σημαίνει ότι ο πρώτος και ο τρίτος στίχος της πρώτης στροφής ομοιοκαταληκτούν και επαναλαμβάνονται αυτούσιοι ή ελαφρώς παραλλαγμένοι εναλλάξ στις υπόλοιπες τέσσερις στροφές ως ρεφρέν και συνθέτουν τους δύο τελευταίους στίχους της τελικής τετράστιχης στροφής. Χρησιμοποιώντας κεφαλαία γράμματα για τα ρεφρέν και πεζά γράμματα για τις ρίμες, η μορφή μπορεί να εκφραστεί μαθηματικά ως εξής:
Δομή Βιλανέλας |
|||
Στίχοι/ Στροφές |
Ρίμα |
Ρεφρέν |
Τελική Μορφή |
1 |
α |
Α1 |
α/ Α1 |
2 |
β |
|
β |
3 |
α |
Α2 |
α/ Α2 |
4 |
α |
|
α |
5 |
β |
|
β |
6 |
α |
Α1 |
α/ Α1 |
7 |
α |
|
α |
8 |
β |
|
β |
9 |
α |
Α2 |
α/ Α2 |
10 |
α |
|
α |
11 |
β |
|
β |
12 |
α |
Α1 |
α/ Α1 |
13 |
α |
|
α |
14 |
β |
|
β |
15 |
α |
Α2 |
α/ Α2 |
16 |
α |
|
α |
17 |
β |
|
β |
18 |
α |
Α1 |
α/ Α1 |
19 |
α |
Α2 |
α/ Α2 |
Και συνοπτικά: A1 β A2 / α β A1 / α β A2 / α β A1 / α β A2 / α β A1 A2.
Αν η μορφή θυμίζει τραγούδι, αυτό συμβαίνει γιατί πράγματι αρχικά επρόκειτο για τραγούδια τα οποία τραγουδούσαν οι Villani (χωρικοί) της Ιταλίας, από όπου και το όνομα.
Η βιλανέλα, λοιπόν, είναι παλιά κλασική και μελωδική ποιητική μορφή, της οποίας οι στίχοι ακολουθούν αυστηρό μέτρο και των οποίων οι στροφές σχηματίζονται από πλέξιμο στοιχείων ρίμας και ρεφρέν, με τρόπο που μοιάζει με τα συνδυασμένα κύματα ημιτονοειδούς και συνημιτονοειδούς συνάρτησης στο επίπεδο, όπως θα δούμε. Η ποιητική αυτή μορφή είναι δύσκολο να χρησιμοποιηθεί επιτυχώς και απαιτεί ορισμένες προσαρμογές στην επιλογή λέξεων και φράσεων καθ’ όλη τη διαδικασία δημιουργίας του ποιήματος.
Βιλανέλες έχουν γράψει μεταξύ άλλων οι Γ.Χ. Ώντεν, Ντύλαν Τόμας, Όσκαρ Γουάιλντ, Σέιμους Χήνυ, Σύλβια Πλαθ, Τζαίημς Τζόυς, Τόμας Χάρντυ, και στα Ελληνικά παλαιότερα οι Μ. Τσιριμώκος και Γ. Σαραλής, ενώ πρόσφατα ο Χ. Βλαβιανός.
-
Βιλανέλα και Μαθηματικά
Γιατί αξίζει να ασκούμαστε στη γραφή βιλανέλας; Πώς σχετίζεται με τα Μαθηματικά; Η απάντηση κρύβεται στα βάθη της περιοδικότητας, που είναι ‘συμμετρία στον χρόνο’ -αλλά ξέρουμε ότι ο χρόνος πάντα προχωράει και ποτέ δεν γυρίζει πίσω. Τι εννοούμε με τη ‘συμμετρία στον χρόνο’; Η δομή μιας βιλανέλας, και η προσπάθεια και η έμπνευση γραφής της, βοηθά στην απάντηση σε αυτές τις ερωτήσεις.
Ας δούμε μια βιλανέλα από τον W. H. Auden, είναι η “If I could tell you”:
H. Auden / If I Could Tell You
Time will say nothing but I told you so,
Time only knows the price we have to pay;
If I could tell you I would let you know.
If we should weep when clowns put on their show,
If we should stumble when musicians play,
Time will say nothing but I told you so.
There are no fortunes to be told, although,
Because I love you more than I can say,
If I could tell you I would let you know.
The winds must come from somewhere when they blow,
There must be reasons why the leaves decay;
Time will say nothing but I told you so.
Perhaps the roses really want to grow,
The vision seriously intends to stay;
If I could tell you I would let you know.
Suppose all the lions get up and go,
And all the brooks and soldiers run away;
Will Time say nothing but I told you so?
If I could tell you I would let you know.
[October 1940]
Ακολουθεί μια βιλανέλα που γράφτηκε πρόσφατα, χρησιμοποιώντας το ίδιο σχήμα ποιήματος με τον Auden, για να πούμε αντίο στο αεροδρόμιο:
Emily Grosholz / Holding Pattern
We can’t remember half of what we know.
They hug each other and then turn away.
One thinks in silence, never let me go.
The sky above the airport glints with snow
That melts beneath the laws it must obey.
We can’t remember half of what we know.
His arms are strong and warm, his breath is slow;
She holds him close, not knowing what to say.
One thinks in silence, never let me go.
Time silts the rivers, ravaging the flow
Of wave on a wavelet, and suspends the day.
We can’t remember half of what we know.
This holding is an agreement to forego,
This flight another strategy to stay.
One thinks in silence, never let me go.
The silver trees spring back to life, although
Their roots are gilded by the leaves’ decay.
We can’t remember half of what we know,
One thinks in silence. Never let me go.
Το ενδιαφέρον με τη δομή της βιλανέλας είναι ότι απαιτεί ένα μοτίβο/ πρότυπο ρίμας (και συνεπώς μέτρο), αλλά επίσης -με τον τρόπο του τραγουδιού- την επανάληψη ολόκληρων στίχων, ως ρεφρέν. Αυτή η συμβολή δημιουργεί ενδιαφέρουσες υπερθέσεις διαφορετικών ειδών περιοδικότητας: την επανάληψη του ήχου (φωνήματα), του τυπικού στίχου (που ορίζεται από το μέτρο), και σημαντικών γραμματικών ενοτήτων (οι φράσεις/ στίχοι που επαναλαμβάνονται).
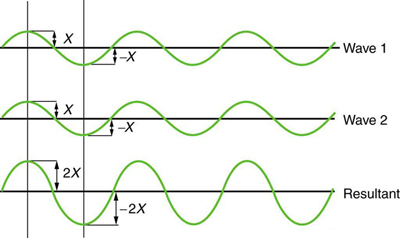
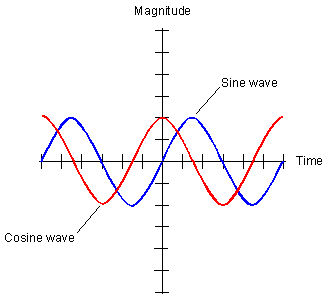
Το μαθηματικό σχήμα για το περιοδικό μοτίβο είναι το ημιτονοειδές κύμα: ένα δεδομένο ημιτονοειδές κύμα έχει ορισμένο πλάτος (πόσο μεγάλο ή έντονο είναι) και συγκεκριμένη συχνότητα (πόσο γρήγορα οι κορυφές του περνούν από ένα δεδομένο σταθερό σημείο). Ένα συνημιτονοειδές κύμα έχει το ίδιο σχήμα, αλλά με μετατόπιση/ διαφορά φάσης. Όταν δύο ημιτονοειδή ή συνημιτονοειδή κύματα διαφορετικού πλάτους και συχνότητας υπερτίθενται, δημιουργούν ένα νέο μοτίβο, με ιδιαίτερα υψηλές κορυφές σε σημεία όπου αυτές των αρχικών κυμάτων τυχαίνει να ενισχύουν η μια την άλλη, ιδιαίτερα χαμηλές κορυφές όταν αυτές υπερτίθενται, και ένα σύνθετο αλλά κανονικό μείγμα εύρους ενδιάμεσα. Οποιαδήποτε περιοδική συνάρτηση, ανεξάρτητα από το πόσο φαίνεται ακανόνιστη, μπορεί να αναπαρασταθεί από ένα (πιθανώς άπειρο) άθροισμα ημιτονοειδών και συνημιτονοειδών συναρτήσεων, το οποίο στα Μαθηματικά ονομάζεται μετασχηματισμός Fourier.
Ημιτονοειδές (sine) συνημιτονοειδές (cosine) κύμα // Υπέρθεση
Πώς μπορούν οι ποιητές να χρησιμοποιήσουν τη μαγεία αυτής της υπέρθεσης; Ένα προφανές παράδειγμα αυτού είναι η διαφορά μεταξύ τερματικών στίχων και στίχων που παρουσιάζουν ασθενέστερα και ισχυρότερα είδη διασκελισμού -η συνέχιση μιας πρότασης χωρίς παύση πέρα από το τέλος ενός στίχου-, φαινόμενο κατά το οποίο το νόημα, η φράση ή μια λέξη δεν ολοκληρώνεται σε ένα στίχο αλλά συνεχίζεται και στον επόμενο. Η στιχοποιία των ποιημάτων, αφενός, δημιουργεί μια τυπική περιοδικότητα, αλλά, αφετέρου, η γραμματική έχει τη δική της περιοδικότητα, που σηματοδοτείται από την ολοκλήρωση μιας πρότασης, το κεφαλαίο γράμμα στην αρχή, την τελεία στο τέλος και ένα κενό διάστημα πριν από την επόμενη πρόταση.
Αυτά τα δύο είδη περιοδικότητας, που προέρχονται από τη δομή της βιλανέλας και τη γραμματική γενικά, μπορεί να συμπίπτουν, όπως συμβαίνει σε προσεκτικά σχεδιασμένους τελικούς στίχους, ή στις μορφές που επέλεξαν οι βάρδοι εδώ και αιώνες από την προφορική παράδοση -ωστόσο, μπορεί και όχι. Η γραμματική δομή των διασκελισμένων στίχων ξεχειλίζει και παραβιάζει τα όρια που θέτει ο ποιητικός στίχος, δημιουργώντας ένταση μεταξύ της σκέψης που εκφράζεται και της μορφής. Αντίθετα, τα όρια που θέτει ο ποιητικός στίχος μπορεί να διακόψουν τη γραμματική δομή με τρόπους που ενισχύουν και τονίζουν λέξεις ή φράσεις, ή τις υπονομεύουν και τις αναλύουν με ειρωνικό τρόπο.
Οι άνθρωποι που εκλαμβάνουν την περιοδικότητα ως επανάληψη δεν μπορούν ποτέ να ξεχάσουν τη διαφορά που δίνει τις αποχρώσεις στην ομοιότητά τους. Είμαστε σε θέση να χρησιμοποιούμε περιοδικότητες για να νιώσουμε άνετα στον κόσμο, αλλά μόνο επειδή τις γνωρίζουμε και τις αναπαριστούμε -και η σκιερή πλευρά της γνώσης και της αναπαράστασης είναι ο θάνατος. Οι κύκλοι της περιοδικότητας είναι πραγματικά σπειροειδείς, απλωμένοι κατά μήκος του βέλους του χρόνου που πετάει μόνο προς μία κατεύθυνση και αργά ή γρήγορα ρίχνει κάτω κάθε πλάσμα -η περιοδικότητα είναι ‘συμμετρία στον χρόνο’, δυναμική και όχι στατική.
Τελειώνω με μια σύγχρονη ελληνική βιλανέλα που διεκτραγωδεί τα βάσανα του ποιητή, αλλά και της Μούσας του:
Χάρης Βλαβιανός / Βιλανέλα Πικρή χωρίς Βανίλια
Δεκαέξι μήνες τώρα ούτε έναν στίχο.
Η Μουσίτσα σου με άλλον θα ερωτοτροπεί.
Κι έτσι η έμπνευσή σου χτύπησε σε τοίχο.
Εσύ: «Δε με λυπάσαι; Όλη μέρα βήχω!».
Εκείνη: «Κι άλλη λευκή σελίδα; Τι ντροπή!».
Δεκαέξι, αχ, μήνες τώρα ούτε έναν στίχο.
Βαριά η νύχτα. Δεν ακούς κανέναν ήχο.
Η υπόθεση έχει πάρει πια κακή τροπή
αφότου η έμπνευσή σου χτύπησε σε τοίχο.
«Κάνε επιτέλους κάτι και μην είσαι ψυχο-
βγάλτης! Θέλεις η σχέση μας έτσι να κοπεί;».
«Μα τόσους μήνες τώρα ούτε έναν στίχο
δεν έχω αξιωθεί. Δεν είμαι στιχο-
πλόκος! Είναι η απόρριψη πολύ νωπή».
«Μα αφού η έμπνευσή σου χτύπησε σε τοίχο
σκέψου το λίγο ακόμα προτού φύγω
λες αυτή να ’ναι της ζωής σου η ροπή;
Επί δεκαέξι χρόνια ούτε έναν στίχο
η έμπνευσή σου να χτυπά (πάντα) σε τοίχο!».
[Αυτοπροσωπογραφία του Λευκού. Πατάκης, 2018].
Από την άποψη της τεχνικής, αν κάνει κάποιος τον κόπο να συγκρίνει τη δομή αυτής της βιλανέλας με το πιο πάνω αναφερόμενο πρότυπο, βλέπει ότι ταυτίζεται πλήρως με αυτό. Από την άποψη της ουσίας, προβάλλεται το γεγονός ότι κινούμαστε σε σπειροειδείς τροχιές, όπου συνυπάρχει ο κύκλος και η ευθεία, η περιοδικότητα και η εξέλιξη, όπου μπορούμε να βλέπουμε τη σταθερότητα και τη μεταβολή, άλλοτε με ηδονή και άλλοτε με οδύνη. Ο χρόνος έχει µια κατεύθυνση, ταξιδεύει εµπρός σαν βέλος. Η φράση ‘το βέλος του χρόνου’ -την ανέφερε πρώτος ο αστροφυσικός Arthur Eddington το 1927- δείχνει τη μονοσήμαντη φορά του χρόνου, δίνει την αίσθηση της προσωρινότητας, όπως την εκφράζει ο Προυστ στο Αναζητώντας τον Χαµένο Χρόνο. ‘Άδραξε τη μέρα’ λένε οι ποιητές, ‘carpe diem’ γιατί ο χρόνος περνά χωρίς αντιστροφή. Ο θάνατος είναι η απτή μαρτυρία για την ροή του χρόνου: η µη αντιστρεπτότητα του χρόνου.
Ελπίζω μόνο ο ποιητής να βρήκε πιο ‘αποτελεσματική’ Μούσα.
Το προαναφερόμενο άρθρο είναι το:
Emily R. Grosholz and Sarah Glaz (2019). How to Use Prime Numbers and Periodicity to Write a Poem. Bridges 2019 Conference Proceedings, 643-646.