- Όμορφες Σχέσεις
Μιλώντας για την ομορφιά των μαθηματικών σχέσεων, τίθεται το ερώτημα για τις Όμορφες Σχέσεις.
1η στην κλίμακα ομορφιάς, στην υψηλότερη θέση, βρίσκεται η ταυτότητα του Euler:
eiπ + 1 = 0,
η οποία, παρά την απλότητά της, εμπλέκει τις σημαντικότερες πέντε μαθηματικές σταθερές μέσω των τριών βασικών αριθμητικών πράξεων.
2η το Θεώρημα του Πυθαγόρα:
α2 + β2 = γ2.
3η οι σχέσεις Cauchy-Riemann στη Μιγαδική Ανάλυση:
∂u/ ∂x = ∂v/ ∂y, ∂u/ ∂y = − ∂v/ ∂x.
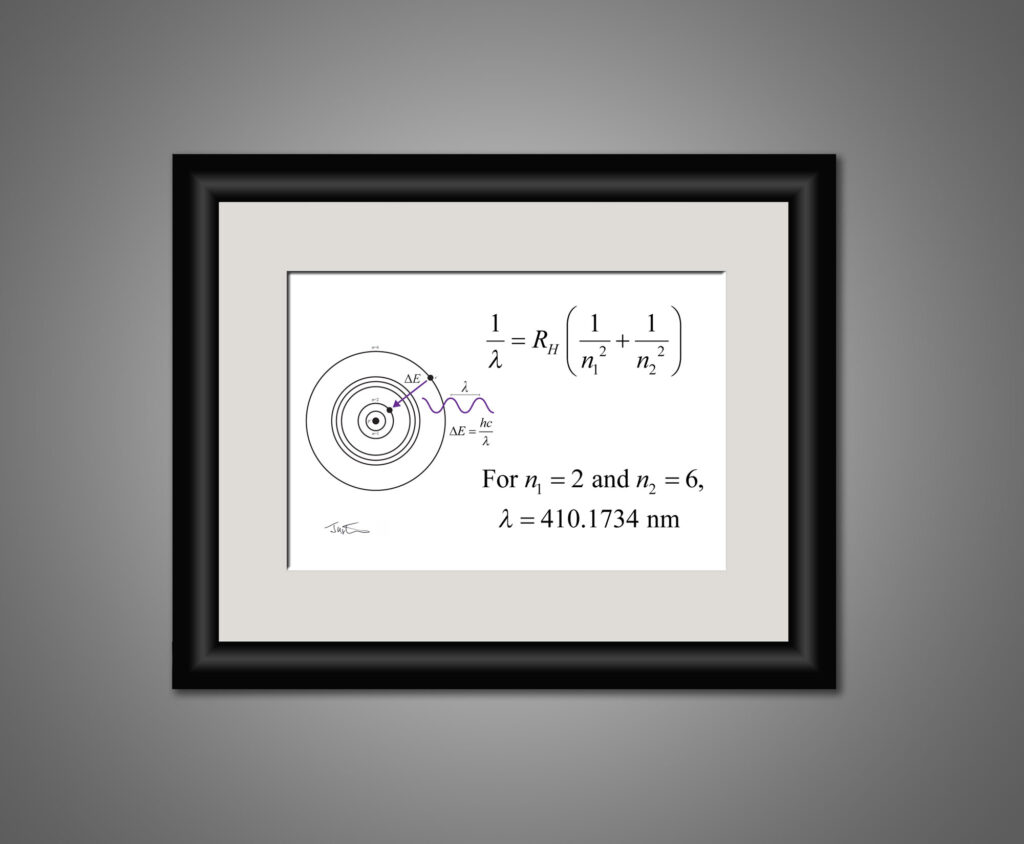
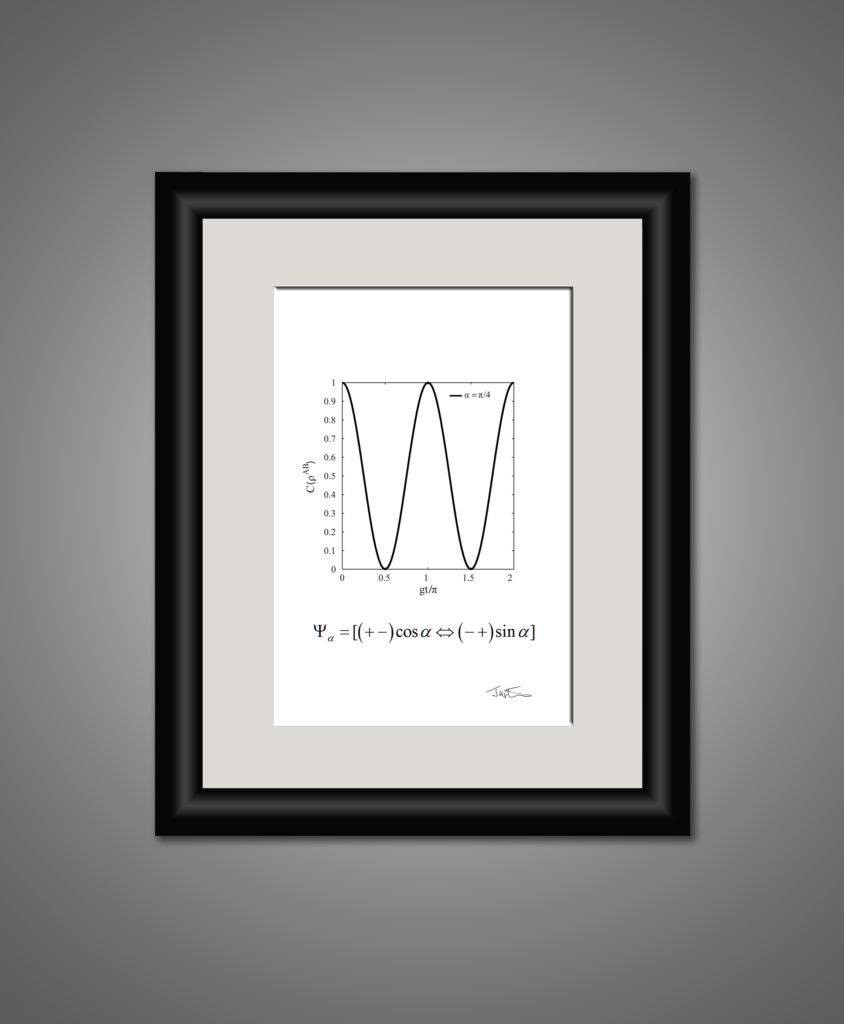
Ο φωτογράφος Justin Mullins το 2010 έκανε στην Αυστραλία μια πρωτότυπη έκθεση φωτογραφιών των πιο σημαντικών εξισώσεων, το ίδιο και τον Οκτώβρη 2019 στο Λονδίνο. Λέει επ’ αυτού: “Εγώ δεν είμαι μαθηματικός. Για μένα, οι διανοητές που συνέταξαν τις εξισώσεις μοιάζουν με τους μεγάλους εξερευνητές που επιστρέφουν από μακρινές παραλίες και μιλούν για φανταστικούς τόπους και μαγικά πλάσματα”. Ο καλλιτέχνης ανέλαβε να αφηγηθεί αυτές τις εξισώσεις, να τις απομυθοποιήσει, να τις φωτογραφίσει, να τις χωρίσει σε κατηγορίες και να τις δείξει στο ευρύ κοινό. Τον τίτλο της πιο όμορφης εξίσωσης θεωρεί και αυτός ότι δικαιούται η ταυτότητα του Euler –“είναι σαν το Γκραν Κάνιον, το Έβερεστ και τους Καταρράκτες του Νιαγάρα μαζί: το τι βλέπεις εξαρτάται από τη γωνία υπό την οποία το κοιτάς”.
- Μαθηματικά και Αισθητική: Αισθητικό Μέτρο και Τύπος του Birkhoff
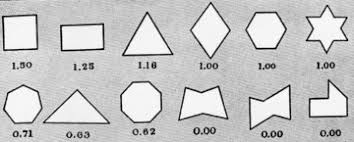
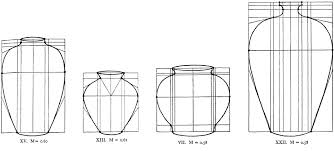
Βασική θέση του μαθηματικού George David Birkhoff (1933) είναι ότι το αισθητικό μέτρο εξαρτάται από την πυκνότητα των στοιχείων τάξης στο αντικείμενο που εξετάζουμε. Ο Birkhoff προσδιορίζει έναν παράγοντα, τον οποίο ονομάζει ‘αισθητικό μέτρο’ (Μ), που εξετάζει δυο στοιχεία: την αισθητική τάξη (Order: Ο) και την πολυπλοκότητα (Complexity: C):
Μ = Ο/C.
Η αισθητική τάξη κατά Birkhoff δίνεται από την τάξη/ κανονικότητα των στοιχείων που συνιστούν το αντικείμενο μελέτης, ενώ η πολυπλοκότητα μετρά την μεγαλύτερη ή την μικρότερη παρουσία των εν λόγω στοιχείων. Μπορεί κάποιος να παρατηρήσει από τον παραπάνω τύπο ότι όσο μεγαλύτερη είναι η ομορφιά, τόσο μειώνεται η πολυπλοκότητα, δηλαδή ότι υπάρχει ανάλογη σχέση μεταξύ της ομορφιάς και της απλότητας. Ο τύπος του Birkoff εφαρμόζεται για να εκτιμήσει την ομορφιά ποιημάτων, τραγουδιών, γλυπτών, πινάκων ζωγραφικής, ακόμα και ειδών κεραμικής.
- Το Ποιητικό Φαινόμενο ως Μορφογένεση
Το καλοκαίρι του 1981, στο Συμπόσιο Ποίησης στο πανεπιστήμιο της Πάτρας, παρουσίασα μια ‘Αρχική Πρόταση για Μαθηματικοποίηση του Ποιητικού Φαινομένου’. Η πρόταση έλεγε ότι: ‘Το Ποιητικό Φαινόμενο είναι μια Μορφογένεση’. Η Μορφογένεση ορίζεται ως η αλληλουχία διεργασιών/ διαδικασιών που μετασχηματίζει ένα άμορφο, ή με κάποια αρχική μορφή, σύστημα σε ένα άλλο καθορισμένης δομής. Οποιαδήποτε Μορφογένεση συνοδεύεται από δημιουργία Πληροφορίας. Η Πληροφορία προκύπτει από τη διαδοχική επιλογή ‘συμβόλων’ (ή λέξεων) από ένα δοσμένο ‘αλφάβητο’ (ή λεξιλόγιο) προκειμένου να οικοδομηθεί ένα ‘μήνυμα’ (ή κείμενο) με κάποιο νόημα (με μια λογική ‘τάξη’). Η Πληροφορία Ι μετράει τον βαθμό τάξης μέσα στη δομή του μηνύματος, η Εντροπία S μετράει τον βαθμό αταξίας και έχουμε: Ι= -S. Με αυτή την έννοια, η Πληροφορία είναι νεγκεντροπία (negentropy), δηλαδή αρνητική εντροπία. Η ειδοποιός διαφορά μεταξύ μηνυμάτων που περιέχουν ‘πολλή’ ή ‘λίγη’ Πληροφορία είναι το απροσδόκητο και όχι το σπάνιο. Το Ποιητικό Φαινόμενο συνίσταται από την όλη ποιητική διεργασία μαζί με το αποτέλεσμά της, το ποίημα, και συνιστά φαινόμενο αναδυτισμού (emergentism).
- Ερμηνευτικό Πλαίσιο
Λέγοντας, αμέσως πιο κάτω, πλευρίωση (lateralization) εννοούμε την κυριαρχία της μίας πλευράς του σώματος έναντι της άλλης. Οι άνθρωποι αναπτύσσουν σαφή προτίμηση της μίας πλευράς στο σώμα τους, ενώ υπάρχει μία μικρή εξαίρεση ανθρώπων που χρησιμοποιούν με επιτυχία και χωρίς δυσκολίες και τις δύο πλευρές. Η πλευρίωση σχετίζεται με το ποιο από τα δύο ημισφαίρια του εγκεφάλου έχει αποκτήσει λειτουργική υπεροχή.
| Πλευρίωση | |
| Οι διαζευγμένες λειτουργίες ενός κυριολεκτικά ‘σχιζοφρενικού’ όντος | |
| Οι δυο κουλτούρες | |
| Αριστερόστροφη (Αριστερό Ημισφαίριο Εγκεφάλου) | Δεξιόστροφη (Δεξιό Ημισφαίριο Εγκεφάλου) |
| STEM
(Science – Technology – Engineering – Mathematics ) |
HUMANITIES
(Ανθρωπιστικές, Κοινωνικές, Θεωρητικές Σπουδές) |
| Κριτήριο ‘αλήθειας’ | Κριτήριο ‘ομορφιάς’ |
| Επιστήμη | Θρησκεία |
| Τεχνολογία | Τέχνη |
| Μαθηματικά | Ποίηση |
| Έρευνα | Φιλοσοφία |
| Πρόσβαση στη ‘Φύση’ | Πρόσβαση στον ‘Θεό’ |
| Γλώσσα της ‘λογικής’ | Γλώσσα ‘μυστικιστικού’ τύπου |
| Υπερκώδικας/ Σύνθεση/ Ολοκλήρωση/ Συμπληρωματικότητα/ Πληρότητα | |
| “Ars sine scientia nihil est” / “Contraria sunt complementaria” | |
| Ενότητα και Συμπληρωματικότητα συνιστούν την πραγματικότητα (Heisenberg) | |
- Ασυμμετρίες Ψυχής τε και Σώματος
Υπάρχει δυσαρμονία/ ασυμμετρία στη δομή του εγκεφάλου (εγκεφαλική ασυμμετρία) και οι νευρωνικές διασυνδέσεις είναι μάλλον ελλιπείς σε ό,τι αφορά την απρόσκοπτη αμοιβαία διακίνηση ηλεκτροχημικών ερεθισμάτων και ουσιών -ορμονών, νευροδιαβιβαστών, νευροπεπτιδίων κλπ. Αποτέλεσμα είναι τα δυο υποσυστήματα να απολαμβάνουν σχετικής αυτονομίας με επακόλουθο την ατελή συνεργασία τους.
Η ‘διαμάχη’, ανάμεσα στις παρορμήσεις, τα συναισθήματα κτλ. από τη μια πλευρά (Ποίηση) και τη λογική σκέψη από την άλλη (Μαθηματικά), αποδίδεται στην ενδογενή φυλογενετική δυσαρμονία της δομής του ανθρώπινου εγκεφάλου. Η διαπάλη αυτή χαρακτηρίζει κάθε άνθρωπο κάθε εποχής, εκδηλώνεται με οξείες και ήπιες φάσεις και σε τελευταία ανάλυση αντικατοπτρίζει το ανισότροπο και ασυμβίβαστο ανάμεσα στα διαλαμβανόμενα στα δύο διαφορετικά επίπεδα. Αντίστοιχες ασυμμετρίες παρατηρούνται και στο ψυχικό σύστημα μεταξύ συνειδητού και ασυνειδήτου. Δυστυχώς ως ανθρώπινη φυλή, την παραπάνω αναγκαία σύνθεση δεν έχουμε πετύχει ακόμα.
- Γνωστική Προσέγγιση
Ένα από τα σύγχρονα προβλήματα στο πεδίο της γνώσης είναι και ο κατακερματισμός της. Η διαθεματικότητα/ διεπιστημονικότητα προτείνεται ως μια κάποια λύση στο πρόβλημα αυτό. Η συνθετική θεώρηση Ποίησης και Μαθηματικών βοηθάει προς την κατεύθυνση της υπέρβασης του κατακερματισμού και των γνωστικών στεγανοποιήσεων στην εκπαίδευση και στην κοινωνία. Η συνειδητοποίηση των αλληλεπιδράσεων και των στενών σχέσεων ανάμεσα στα Μαθηματικά και την Ποίηση συμβάλλει στο να ξεπεραστεί το πολωτικό σχήμα που κυριαρχεί στο μυαλό μαθητών και δασκάλων και κατ’ επέκταση των απλών ανθρώπων, οι οποίοι αντιμετωπίζουν την Ποίηση και τα Μαθηματικά ως ξένες και ασύμβατες περιοχές. Η πρακτική εφαρμογή όλων αυτών αναιρεί την κοινή αντίληψη για το ασυμβίβαστο Μαθηματικών και Ποίησης, συμβάλλοντας έτσι αφενός στην προσπάθεια αντιμετώπισης της μαθηματικοφοβίας και του φόβου μπροστά στη μαθηματική απόδειξη, και αφετέρου στην συνειδητοποίηση της ενότητας και ολότητας της γνωστικής λειτουργίας και στο πρόβλημα των δυο πολιτισμών.