- ΥΛΙΚΟ
Η Ιρακινοαμερικανίδα ποιήτρια Dunya Mikhail γεννήθηκε στη Βαγδάτη το 1965 και απέκτησε πτυχίο στο Πανεπιστήμιο της Βαγδάτης. Εργάστηκε ως μεταφράστρια και δημοσιογράφος πριν συμπεριληφθεί στη λίστα των εχθρών του καθεστώτος. Μετανάστευσε στις Ηνωμένες Πολιτείες στα μέσα της δεκαετίας του 1990 και απέκτησε μεταπτυχιακό στο Wayne State University. Διδάσκει στο Πανεπιστήμιο του Όκλαντ στο Μίσιγκαν. Οι τιμές της Mikhail περιλαμβάνουν το Βραβείο Ανθρωπίνων Δικαιωμάτων των Ηνωμένων Εθνών για την ελευθερία της γραφής. Βραβευμένη με το Βραβείο UNESCO-Sharjah για τον Αραβικό Πολιτισμό, έχει επίσης λάβει υποτροφίες από καλλιτέχνες των Ηνωμένων Πολιτειών, το Ίδρυμα Μνήμης Guggenheim Δημιουργικών Τεχνών και το Ίδρυμα Kresge.
Η Dunya Mikhail είναι συγγραφέας πολλών ποιητικών συλλογών:
The War Works Hard (New Directions, 2005),
Το Diary of a Wave Outside the Sea (New Directions, 2009),
The Iraqi Nights (New Directions, 2014),
In Her Feminine Sign (New Directions, 2019),
Tablets: Secrets of the Clay (New Directions, 2024).
Έγραψε επίσης το μη λογοτεχνικό βιβλίο The Beekeeper (New Directions, 2018), και
το πρώτο της μυθιστόρημα, The Bird Tattoo (Pegasus Books, 2022).
*
Dunya Mikhail / The Theory of Absence
The hypothesis:
I am tense and so are you.
We neither meet nor separate.
The desired result:
We meet in the absence.
The proof:
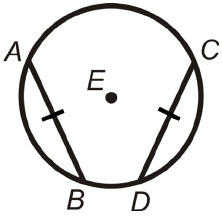
As tension turns people into arcs, we are two arcs.
We neither meet nor separate (the hypothesis)
so, we must be parallel.
If two parallel lines are bisected by a third line
(in this case, the line of tension)
their corresponding angles must be equal (a geometrical theorem).
So we are congruent (because shapes are congruent
when their angles are equal)
and we form a circle (since the sum
of two congruent arcs
is a circle).
Therefore we meet in the absence
(since the circumference of a circle
is the sum of contiguous points
which can each be considered
a point of contact).
Dunya Mikhail / Η Θεωρία της Απουσίας
Η υπόθεση:
Είμαι σε ένταση το ίδιο και εσύ.
Ούτε συναντιόμαστε ούτε χωρίζουμε.
Το επιθυμητό συμπέρασμα:
Συναντιόμαστε στην απουσία.
Η απόδειξη:
Καθώς η ένταση μετατρέπει τους ανθρώπους σε τόξα, είμαστε δύο τόξα.
Ούτε συναντιόμαστε ούτε χωρίζουμε (η υπόθεση)
άρα, πρέπει να είμαστε παράλληλοι.
Αν δύο παράλληλες ευθείες τέμνονται από τρίτη ευθεία
(σε αυτή την περίπτωση, η γραμμή έντασης)
οι αντίστοιχες γωνίες τους πρέπει να είναι ίσες (γεωμετρικό θεώρημα).
Άρα είμαστε σύμφωνοι (επειδή τα σχήματα είναι ομοιόμορφα
όταν οι γωνίες τους είναι ίσες)
και σχηματίζουμε κύκλο (αφού το άθροισμα
δύο ίσων τόξων
είναι κύκλος).
Επομένως συναντιόμαστε στην απουσία
(αφού η περιφέρεια ενός κύκλου
είναι το άθροισμα των συνεχόμενων σημείων
που το καθένα μπορεί να θεωρηθεί
ένα σημείο επαφής).
- ΣΧΟΛΙΑ
(i) Για την Ποιήτρια
Με ειρωνεία και ανατρεπτική απλότητα, η Mikhail πραγματεύεται θέματα πολέμου, εξορίας και απώλειας, χρησιμοποιώντας μορφές όπως ρεπορτάζ, μύθος και στίχοι. Αν και η ποίησή της καταγράφει τα τραύματα του πολέμου και της εξορίας, έχει επίσης μιλήσει για τις επιπτώσεις της λογοκρισίας στο έργο της. Η Mikhail παρατήρησε ότι «στο Ιράκ, υπήρχε ένα τμήμα λογοκρισίας με υπαλλήλους των οποίων η δουλειά ήταν να παρακολουθούν τα ‘δημόσια ήθη’ και να αποφασίζουν τι πρέπει να διαβάζεται και να γράφεται. Κάθε συγγραφέας χρειαζόταν έγκριση πρώτα πριν δημοσιεύσει. Γι’ αυτό χρησιμοποίησα πολλές μεταφορές και στρώματα νοημάτων. Αυτό ήταν πιθανότατα καλό για την ποίησή μου, αλλά, παρ’ όλα αυτά, δεν θέλετε να χρησιμοποιήσετε τέτοια σχήματα λόγου απλώς για να κρύψετε νοήματα. Εδώ, στην Αμερική, μια λέξη συνήθως δεν κοστίζει τη ζωή σε μια ποιήτρια. Ωστόσο, ο λόγος μερικές φορές περιορίζεται σε αυτό που είναι αποδεκτό σύμφωνα με τα δημόσια πρότυπα. Έτσι, στο Ιράκ, το κείμενο προηγείται της λογοκρισίας. Στην Αμερική η ‘λογοκρισία’ προηγείται του κειμένου».
(ii) Για το Ποίημα
Το ‘The Theory of Absence’, επιλογή από τη συλλογή The War Works Hard,
διατυπώνοντάς το με φαινομενικά στεγνό και κλινικό τρόπο, η Dunya Mikhail κάνει το δίλημμα που αποτυπώνεται στο ποίημα περισσότερο ή λιγότερο συναισθηματικά γεμάτο.
Με τους υπότιτλους, «Η υπόθεση:», «Το επιθυμητό συμπέρασμα:», «Η απόδειξη:»,
αναπαριστά την τεταμένη κατάσταση ανάμεσα σε δύο άτομα. Η τεταμένη κατάσταση μεταξύ δύο προσώπων (αντίπαλοι; ένα ζευγάρι; και τα δύο;) οριοθετείται με ψυχρό και κυριολεκτικά υπολογισμένο τρόπο από τη μια πλευρά. Ταυτόχρονα, η παρουσίαση της κατάστασης ως ένα μαθηματικό πρόβλημα της δίνει την υπονοούμενη δύναμη μιας καθολικά κατανοητής –και επομένως επιλύσιμης– έννοιας. Αυτό σημαίνει ότι υπάρχει ελπίδα για αυτό το τεταμένο ζευγάρι;
Στην πραγματικότητα, φαίνεται ότι η Mikhail έδωσε σε αυτό το ποίημα έντονο συναισθηματικό βάρος, με την αντίθετη διαισθητική μέθοδο, για να το αποστραγγίσει από το φαινομενικό συναίσθημα. Μέχρι να φτάσουμε στον στίχο «Άρα είμαστε σύμφωνοι», ίσως έχουμε την αίσθηση ότι το ποίημα είναι χρωματισμένο με χιούμορ. Ίσως ακόμη και να ψάχνουμε για το τι περιγράφει το ποίημα. Έχει καλό νόημα;
Τέλος, καθώς το ποίημα ολοκληρώνεται με «ένα σημείο επαφής», τα πράγματα τελειώνουν αναμφισβήτητα με μια αισιόδοξη νότα. Η τεταμένη κατάσταση μπορεί να επιλυθεί. Απλώς έπρεπε να διατυπωθεί λογικά, ως εξίσωση ή μαθηματική σχέση. Η ιδιαίτερη δεξιότητα της ποιήτριας είναι η προβολή άκοσμων/ αστόλιστων εικόνων που αποτυπώνουν τις συχνά απροσδόκητες ανθρώπινες αντιδράσεις και αλληλεπιδράσεις.
(iii) Για τα Μαθηματικά του Ποιήματος
Το κέντρο του κειμένου είναι φυσικά το ποίημα και το αν επιτυγχάνει τον ποιητικό σκοπό του και επιτελεί την ποιητική λειτουργία του. Αν όμως ο ποιητής χρησιμοποιεί μαθηματικά στοιχεία, τότε ο μαθηματικός μπαίνει στον πειρασμό να τα εξετάσει. Από αυτή την άποψη, έχω την εντύπωση ότι υπάρχουν κάποια προβλήματα και κάποια ασάφεια. Δεν μπαίνω σε λεπτομέρειες γιατί θα χαθεί ο στόχος, αλλά ως μαθηματικός οφείλω να το επισημάνω.