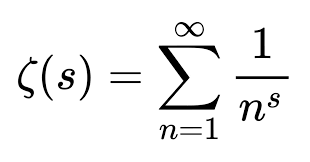- ΥΛΙΚΟ
Ο Τομ Μάικ Άποστολ (Tom Mike Apostol, 1923 – 2016) ήταν Ελληνο- Αμερικανός μαθηματικός, με ειδικότητα στην Ανάλυση και στην Αναλυτική Θεωρία των Αριθμών, και καθηγητής στο Τεχνολογικό Ινστιτούτο της Καλιφόρνια (Κάλτεκ).
Ο Άποστολ γεννήθηκε στην κωμόπολη Χέλπερ της Γιούτα. Οι γονείς του, Εμμανουήλ Αποστολόπουλος και Ευφροσύνη Παπαθανασοπούλου, ήταν Έλληνες μετανάστες. Το ονοματεπώνυμο τού Εμμανουήλ συντομεύθηκε σε «Μάικ Άποστολ» όταν απέκτησε την αμερικανική υπηκοότητα και ο Τομ κληρονόμησε αυτό το αμερικανοποιημένο επώνυμο. Ένας μαθηματικός που στην Ελλάδα δεν ήταν τόσο γνωστός, όμως στην άλλη μεριά του Ατλαντικού δημιούργησε ένα τεράστιο επιστημονικό έργο.
Tom Apostol / Where are the zeros of zeta of s? /
Πού Είναι τα Μηδενικά της Zήτα του s;
(Μπορεί να τραγουδηθεί όπως το ‘Sweet Betsy from Pike’)
| Where are the zeros of zeta of s? G. F. B. Riemann has made a good guess; They’re all on the critical line, saith he, And their density’s one over 2pi log t. |
Πού είναι τα μηδενικά της zeta του s;
Ο Riemann έχει κάνει μια καλή εικασία˙ Είναι όλα στην κρίσιμη γραμμή, λέει ο ίδιος, Και η πυκνότητα τους είναι πάνω από 2pi log t. |
| This statement of Riemann’s has been like a trigger And many good men, with vim and with vigor, Have attempted to find, with mathematical rigor, What happens to zeta as mod t gets bigger. |
Αυτή η δήλωση του Riemann είναι σαν σκανδάλη
Και πολλοί καλοί άντρες, με σφρίγος και σθένος, Έχουν προσπαθήσει να βρουν, με μαθηματική αυστηρότητα, Τι συμβαίνει με τη zeta καθώς το mod t αυξάνει. |
| The efforts of Landau and Bohr and of Cramer, And Littlewood, Hardy and Titchmarsh are there, In spite of their efforts and skill and finesse, (In) locating the zeros there’s been no success. |
Οι προσπάθειες των Landau και Bohr και Cramer,
Και Littlewood, Hardy και Titchmarsh είναι εκεί, Παρά τις προσπάθειές τους, την επιδεξιότητα και τη φινέτσα τους, Στο να εντοπίσουν τα μηδενικά, υπήρξε ελάχιστη επιτυχία. |
| In 1914 G.H. Hardy did find, An infinite number that lay on the line, His theorem however won’t rule out the case, There might be a zero at some other place. |
Το 1914 ο G.H. Hardy το βρήκε,
Ένας άπειρος αριθμός που βρισκόταν στη γραμμή, Ωστόσο, το θεώρημά του δεν αποκλείει την περίπτωση, Ότι μπορεί να υπάρχει μηδέν σε κάποιο άλλο μέρος. |
| Let P be the function pi minus li, The order of P is not known for x high, If square root of x times log x we could show, Then Riemann’s conjecture would surely be so. |
Έστω P η συνάρτηση pi μείον li,
Η τάξη της Ρ δεν είναι γνωστή για μεγάλο x, Εάν μπορούσαμε να δείξουμε την τετραγωνική ρίζα του x επί log x, Τότε η εικασία του Riemann θα ήταν σίγουρα έτσι. |
| Related to this is another enigma, Concerning the Lindelof function mu(sigma) Which measures the growth in the critical strip, On the number of zeros it gives us a grip. |
Σχετικά με αυτό είναι ένα άλλο αίνιγμα,
Θεωρώντας τη συνάρτηση Lindelof mu(sigma) Η οποία μετρά την αύξηση στην κρίσιμη γραμμή, του αριθμού των μηδενικών, μας δίνει μια λαβή. |
| But nobody knows how this function behaves, Convexity tells us it can have no waves, Lindelof said that the shape of its graph, Is constant when sigma is more than one-half. |
Αλλά κανείς δεν ξέρει πώς συμπεριφέρεται αυτή η συνάρτηση,
Η κυρτότητα μας λέει ότι δεν μπορεί να έχει κυμάνσεις, Ο Lindelof είπε ότι το σχήμα του γραφήματός του, Είναι σταθερό όταν το σίγμα είναι μεγαλύτερο από το μισό. |
| Oh, where are the zeros of zeta of s? We must know exactly, we cannot just guess, In order to strengthen the prime number theorem, The integral’s contour must not get too near ’em. |
Ω, πού είναι τα μηδενικά της zeta του s;
Πρέπει να γνωρίζουμε ακριβώς, δεν μπορούμε απλώς να μαντέψουμε, Προκειμένου να ενισχυθεί το θεώρημα των πρώτων αριθμών, Η καμπύλη του ολοκληρώματος δεν πρέπει να τους πλησιάζει πολύ. |
- ΣΧΟΛΙΑ
(i) Η Υπόθεση Riemann σε Τραγούδι
Ο Tom Apostol, Καθηγητής Μαθηματικών τότε στο Caltech, έγραψε το ποίημα για την Υπόθεση Riemann (RH) το 1955. Οι αρχικοί στίχοι του Apostol έφτασαν μόνο μέχρι τον στίχο 32 (8×4: οχτώ τετράστιχα), οι τελευταίες στροφές αναρτήθηκαν στο Πανεπιστήμιο του Κέιμπριτζ το 1973 από τον άλλο μεγάλο μαθηματικό Saunders MacLane (δες στο τέλος του κειμένου).
Το τραγούδι αναφέρει την Υπόθεση Lindelöf (LH), νεότερο ξάδερφο του RH, που χρονολογείται από το 1908, αλλά επειδή είναι περιφερειακό της κύριας ιστορίας και περιλαμβάνει ειδική σημειογραφία και επειδή το ποίημα είχε ήδη πάρα πολλά μαθηματικά σε εκείνο το σημείο, το άφησε έξω. Ωστόσο, οι στίχοι του Apostol δεν μπορούν να γίνουν κατανοητοί χωρίς αυτό, και δεν άντεχα να τους παραλείψω, οπότε παίρνεις ένα τραγούδι και μια Υπόθεση μπόνους.
(ii) Το Κυνήγι των Πρώτων
Από την εποχή του Ερατοσθένη, εφευρέθηκαν πολλές τεχνικές για να ‘πιάσουν’ πρώτους αριθμούς, αλλά μέχρι στιγμής δεν έχει βρεθεί φόρμουλα που να τους καλύπτει όλους. Συγκεκριμένα, είναι εξαιρετικά δύσκολο να παράγουμε πολύ μεγάλους πρώτους. Κανένα μοτίβο δεν βρέθηκε να προβλέπει την κατανομή τους εντός δεδομένου διαστήματος αριθμών.
Το 2000, το Ινστιτούτο Μαθηματικών Clay απαριθμεί επτά από τα πιο σημαντικά ανοιχτά προβλήματα στα Μαθηματικά. Ένα πρόβλημα, η υπόθεση Riemann, που διατυπώθηκε από τον Bernhard Riemann, γιόρτασε την 150η επέτειό του το 2010. Είναι μια εικασία για τα μηδενικά της συνάρτησης Riemann zeta. Η συνάρτηση ζ ορίζεται για μιγαδικές μεταβλητές, s, και μια τιμή s για την οποία ζ(s) = 0 καλείται μηδέν της zeta. Η συνάρτηση zeta εισήχθη από τον Leonhard Euler στις αρχές του 1800 ως συνάρτηση μιας πραγματικής μεταβλητής. Ο Riemann επέκτεινε τη συνάρτηση σε μιγαδικούς αριθμούς και καθιέρωσε μια σύνδεση μεταξύ του συνόλου μηδενικών και των ιδιοτήτων των πρώτων αριθμών. Η υπόθεση Riemann θεωρείται ως το πιο σημαντικό ανοιχτό πρόβλημα στα καθαρά Μαθηματικά και η λύση του θα προωθούσε τις γνώσεις μας για την κατανομή των πρώτων αριθμών. Το ποίημα του Tom Apostol “Where Are the Zeros of Zeta of s?”, μεταδίδει παιχνιδιάρικα τον ενθουσιασμό που δημιουργείται από το κυνήγι για τη λύση του. Πολλές άλλες ερωτήσεις σχετικά με τους πρώτους αριθμούς παραμένουν αναπάντητες. Μερικά από αυτά τα προβλήματα και οι λύσεις τους, καθώς και η μαγεία και το ξόρκι για τους μαθηματικούς που μελετούν τους πρώτους αριθμούς, έχουν επίσης περάσει στην Ποίηση.
(iii) Οι Τελευταίες 7 Συμπληρωματικές Στροφές / New verses by S. MacLane
Now Andy has bettered old Riemann’s fine guess
by using a fancier zeta (s).
He proves that the zeros are where they should be,
provided the characteristic is p.
There’s a moral to draw from this sad tale of woe
which every young genius among you should know:
if you tackle a problem and seem to get stuck,
just take it mod p and you’ll have better luck.
What fraction of zeros on the line will be found,
When mod t is kept below some given bound?
Does the fraction, whatever, stay bounded below,
As the bound on mod t is permitted to grow?
The efforts of Selberg did finally banish,
All fears that the fraction might possibly vanish.
It stays bounded below, which is just as it should,
But the bound he determined was not very good.
Norm Levinson managed to show, better yet,
At two-to-one odds it would be a good bet,
If over a zero you happen to trip,
It would be on the line and not just in the strip.
Levinson tried in a classical way,
Weil brought modular means into play.
Atiyah then left and Paul Cohen quit,
So now there’s no proof at all that will fit.
But now we must study this matter anew,
Serre points out manifold things it makes true.
A medal might be the reward in this quest,
For Riemann’s conjecture is surely the best.
Σημείωση: ακούστε το ‘Sweet Betsy from Pike’ από τον Johnny Cash για να καταλάβετε τον ρυθμό του ποιήματος/ τραγουδιού.