- Υλικό
Βιογραφικό:
Η Τζούντιθ Μπάουμελ (Judith Baumel) είναι Αμερικανίδα ποιήτρια. Γεννήθηκε στις 9 Οκτωβρίου 1956 στο Μπρονξ της Νέας Υόρκης. Έχει γράψει πολλές συλλογές ποιημάτων, μεταξύ των οποίων: “Thorny” (2022), “Passeggiate” (2019), “The Kangaroo Girl” (2011), “Now” (1995) και “The Weight of Numbers” (1988), για την οποία κέρδισε το βραβείο Walt Whitman από την Ακαδημία Αμερικανών Ποιητών. Είναι Ομότιμη Καθηγήτρια Αγγλικών και Ιδρυτική Διευθύντρια του Προγράμματος Δημιουργικής Γραφής στο Πανεπιστήμιο Adelphi. Έχει διατελέσει Πρόεδρος της Ένωσης Συγγραφέων και Προγραμμάτων Συγγραφής, διευθύντρια της Εταιρείας Ποίησης της Αμερικής και υπότροφος Fulbright στην Ιταλία. Έχει αποφοιτήσει από το Bronx High School of Science, το Radcliffe College, το Πανεπιστήμιο του Χάρβαρντ και το Πανεπιστήμιο Johns Hopkins. Έχει σπουδάσει Χημεία και Μαθηματικά.
Ποίημα:
Judith Baumel
Fibonacci
Call it windfall 1
finding your calculation 1
come, finally,
to the last decimal point of pi. 2
In the silence of January snow
a ladybug survives the frost
and appears on the windowpane. 3
She crawls a tiny space.
Hesitant. Reverses. Forward,
like a random-number generator,
the walking computer frog
who entertains mathematicians. 5
Think of the complexity
of temperature, quantification
of that elusive quality “heat”.
Tonight, for instance,
your hands are colder than mine.
Someone could measure
more precisely than we
the nature of this relationship. 8
Learn the particular strength
of the Fibonacci series,
a balanced spiraling
outward of shapes,
those golden numbers
which describe dimensions
of sea shells, rams’ horns,
collections of petals
and generations of bees.
A formula to build
your house on
the proportion most pleasing
to the human eye. 13
*
Τζούντιθ Μπάουμελ
Φιμπονάτσι
Πες το απρόσμενη δωρεά 1
βρίσκοντας τον υπολογισμό σου 1
έλα, επιτέλους,
στο τελευταίο δεκαδικό ψηφίο του πι. 2
Στη σιωπή του Γεναριάτικου χιονιού
μια πασχαλίτσα επιβιώνει στον παγετό
και εμφανίζεται στο τζάμι. 3
Σέρνεται σε ένα μικροσκοπικό χώρο.
Διστακτικά. Αντίστροφα. Μπροστά,
σαν γεννήτρια τυχαίων αριθμών,
ο περιπατών υπολογιστής βάτραχος
που διασκεδάζει τους μαθηματικούς. 5
Σκέψου την πολυπλοκότητα
της θερμοκρασίας, την ποσοτικοποίηση
αυτής της άπιαστης ποιότητας “θερμότητα”.
Απόψε, για παράδειγμα,
τα χέρια σου είναι πιο κρύα από τα δικά μου.
Κάποιος μπορούσε να μετρήσει
με μεγαλύτερη ακρίβεια από εμάς
τη φύση αυτής της σχέσης. 8
Μάθε την ιδιαίτερη δύναμη
της σειράς Φιμπονάτσι,
μια ισορροπημένη σπειροειδή
εξέλιξη σχημάτων,
αυτοί οι χρυσοί αριθμοί
που περιγράφουν διαστάσεις
από κοχύλια, κέρατα κριαριών,
συνδυασμούς πετάλων
και γενιές μελισσών.
Μια φόρμουλα για να χτίσεις
το σπίτι σου πάνω
στην αναλογία που είναι πιο ευχάριστη
στο ανθρώπινο μάτι. 13
- Σχόλια
(i) Ο όρος “Φιμπονάτσι” αναφέρεται στον Λεονάρντο της Πίζας, γνωστό και ως Φιμπονάτσι, έναν Ιταλό μαθηματικό. Έζησε τον 12ο και 13ο αιώνα στην Πίζα της Ιταλίας. Τα ταξίδια του στη Βόρεια Αφρική τον εξέθεσαν στο ινδο-αραβικό σύστημα αρίθμησης. Το βιβλίο του “Liber Abaci” ήταν καθοριστικό για την εισαγωγή του ινδο-αραβικού συστήματος αρίθμησης στους Ευρωπαίους μελετητές και εμπόρους. Περιείχε επίσης το πρόβλημα που οδήγησε στην ακολουθία Φιμπονάτσι.
Είναι διάσημος για:
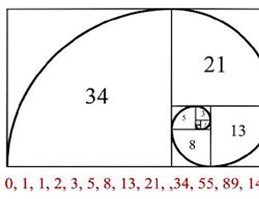
Την ακολουθία Φιμπονάτσι: Πρόκειται για σειρά αριθμών όπου κάθε αριθμός είναι το άθροισμα των δύο προηγούμενων, συνήθως ξεκινώντας από το 0 και το 1. Έτσι, η ακολουθία είναι: 0, 1, 1, 2, 3, 5, 8, 13, 21 και ούτω καθεξής.
Την εισαγωγή του ινδο-αραβικού συστήματος αρίθμησης στην Ευρώπη: Ο Φιμπονάτσι έπαιξε καθοριστικό ρόλο στη διάδοση της χρήσης του ινδο-αραβικού συστήματος αρίθμησης (το δεκαδικό σύστημα που χρησιμοποιούμε σήμερα) στην Ευρώπη μέσω του βιβλίου του “Liber Abaci” (Βιβλίο Υπολογισμού).
Η ακολουθία Φιμπονάτσι στη φύση:
Η ακολουθία Φιμπονάτσι εμφανίζεται σε διάφορα φυσικά φαινόμενα, όπως η διάταξη των φύλλων στα στελέχη, οι σπείρες των κογχυλιών και τα σχέδια των σπόρων στα ηλιοτρόπια. Σχετίζεται επίσης με τη χρυσή τομή.
Σύγχρονες εφαρμογές:
Οι αριθμοί και οι αναλογίες Φιμπονάτσι χρησιμοποιούνται σε διάφορους τομείς, όπως η επιστήμη των υπολογιστών, τα οικονομικά (ιδιαίτερα στην τεχνική ανάλυση των χρηματιστηρίων) και η τέχνη. Εν ολίγοις, ο Φιμπονάτσι ήταν κομβική μορφή στην ιστορία των μαθηματικών και οι συνεισφορές του συνεχίζουν να έχουν σημασία και εφαρμογές σήμερα.
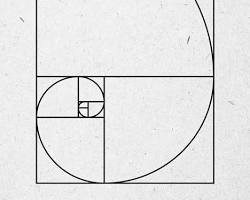
Η ακολουθία Φιμπονάτσι και η χρυσή τομή εμφανίζονται σε πολλά μέρη της φύσης και της τέχνης, δημιουργώντας εντυπωσιακά οπτικά μοτίβα. Υπάρχουν μερικές εικόνες που απεικονίζουν την παρουσία της ακολουθίας Φιμπονάτσι:
Σπείρες κογχυλιών: Η σπείρα ενός κογχυλιού Ναυτίλου εξομοιώνει την ακολουθία Φιμπονάτσι.
Ηλιοτρόπια: Η διάταξη των σπόρων σε ένα ηλιοτρόπιο ακολουθεί την ακολουθία Φιμπονάτσι.
Πέταλα λουλουδιών: Ο αριθμός των πετάλων σε πολλά λουλούδια είναι ένας αριθμός Φιμπονάτσι.
Κλαδιά δέντρων: Ο τρόπος που τα κλαδιά των δέντρων αναπτύσσονται, συχνά ακολουθούν την ακολουθία Φιμπονάτσι.
Χρυσή τομή στην τέχνη: Η χρυσή τομή, που σχετίζεται με την ακολουθία Φιμπονάτσι, χρησιμοποιείται στην τέχνη και την αρχιτεκτονική για να δημιουργήσει αισθητικά ευχάριστες συνθέσεις.
Αυτές οι εικόνες δείχνουν πώς τα μαθηματικά μπορούν να βρεθούν στη φύση και πώς χρησιμοποιούνται στην τέχνη για να δημιουργήσουν όμορφες και αρμονικές συνθέσεις.
(ii) Η σειρά Fibonacci δομικά χρησιμοποιείται ως μοτίβο, ενώ νοηματικά ως μεταφορά για τη φυσική τάξη, την ομορφιά και τις ανθρώπινες σχέσεις.
Η πρώτη στροφή μιλά για την ακρίβεια και την ολοκλήρωση των μαθηματικών: η αναζήτηση του τελευταίου δεκαδικού ψηφίου του π είναι υπενθύμιση ότι οι αριθμοί μπορούν να εκτείνονται άπειρα, αλλά εμείς προσπαθούμε να βρούμε τάξη μέσα στο χάος.
Η εικόνα της πασχαλίτσας στο παράθυρο μέσα στον χειμώνα συμβολίζει το απρόβλεπτο της ζωής. Παρόμοια με μια γεννήτρια τυχαίων αριθμών, η κίνησή της είναι αβέβαιη, όπως και πολλές πτυχές της ύπαρξής μας.
Το θέμα της θερμοκρασίας και της διαφορετικής αίσθησης του κρύου υποδηλώνει ότι ακόμη και τα πιο υποκειμενικά πράγματα μπορούν να μετρηθούν και να ποσοτικοποιηθούν –ακόμα και οι σχέσεις μας.
Η αναφορά στη σειρά Fibonacci επισημαίνει την τελειότητα και την αρμονία που βρίσκουμε στη φύση: στα όστρακα, στα κέρατα των κριαριών, στα πέταλα των λουλουδιών, στις γενιές των μελισσών. Υπονοείται πως αυτή η ισορροπία μπορούσε να είναι και μια μεταφορά για την ανθρώπινη ζωή και τις σχέσεις – ένας ιδανικός, μαθηματικά ισορροπημένος, τρόπος ύπαρξης.
Τελικά, το ποίημα δείχνει τη διαρκή αναζήτηση τάξης και ομορφιάς σε έναν φαινομενικά τυχαίο κόσμο. Η σειρά Fibonacci προσφέρει παράδειγμα αρμονίας, που ίσως μπορούμε να εφαρμόσουμε και στις δικές μας ζωές και σχέσεις.
*Σημείωση
Αυτό είναι ένα ποίημα με δομή δανεισμένη από την ακολουθία Φιμπονάτσι, όμως και το περιεχόμενο σχετίζεται με αυτή. Αν η ποιήτρια ήθελε να εξακολουθήσει το ποίημα, τότε έπρεπε να προσθέσει μια στροφή με 21, μετά με 34 στίχους κτλ.