1. ΥΛΙΚΟ

1.1 ΒΙΟΓΡΑΦΙΚΟ

Ο Χάουαρντ Νεμέροφ ήταν Αμερικανός ποιητής, συγγραφέας και ακαδημαϊκός. Γεννήθηκε την 1 Μαρτίου 1920, Νέα Υόρκη, και απεβίωσε στις 5 Ιουλίου 1991, University City, Μισούρι. Διετέλεσε δύο φορές βραβευμένος Σύμβουλος Ποίησης στη Βιβλιοθήκη του Κογκρέσου (1963 έως 1964 και 1988 έως 1990). Για το The Collected Poems of Howard Nemerov (1977), κέρδισε το National Book Award for Poetry (1977), το Pulitzer Prize for Poetry (1978), και το Bollingen Prize (1981). Έγραψε επίσης μυθιστορήματα και δοκίμια. Κατά τον 2^ο Παγκόσμιο Πόλεμο πολέμησε ως πιλότος μαχητικών αεροσκαφών. Έγινε γνωστός κυρίως για τα ποιήματά του, τα οποία συχνά διερευνούσαν θέματα φύσης, επιστήμης και ανθρώπινης ύπαρξης. Δίδαξε σε διάφορα κολέγια και πανεπιστήμια, συμπεριλαμβανομένου του Πανεπιστημίου Washington στο Σεντ Λούις.

1.2 ΠΟΙΗΜΑ

Howard Nemerov / Figures of Thought

To lay the logarithmic spiral on
Sea-shell and leaf alike, and see it fit,
To watch the same idea work itself out
In the fighter pilot’s steepening, tightening turn
Onto his target, setting up the kill,
And in the flight of certain wall-eyed bugs
Who cannot see to fly straight into death
But have to cast their sidelong glance at it
And come but cranking to the candles flame –

How secret that is, and how privileged
One feels to find the same necessity
Ciphered in forms diverse and otherwise
Without kinship –– that is the beautiful
In Nature as in art, not obvious,
Not inaccessible, but just between.

It may diminish some our dry delight
To wonder if everything we are and do
Lies subject to some little law like that;
Hidden in nature, but not deeply so.

1.3 ΜΕΤΑΦΡΑΣΗ

Χάουαρντ Νεμέροφ / Σκεπτομορφές

Να τοποθετήσεις τη λογαριθμική σπείρα πάνω σε

Θαλασσινό κοχύλι και όμοια σε φύλλο, και να το βλέπεις να ταιριάζει,

να παρατηρήσεις την ίδια ιδέα να εκδηλώνεται

Στον απότομο χειρισμό του πιλότου μαχητικού, σφιχτή στροφή

Προς τον στόχο του, προετοιμάζοντας τη συντριβή του εχθρού,

Και στο πέταγμα ορισμένων εντόμων με στραβισμό

Που δεν μπορούν να δουν να πετάξουν κατευθείαν στον θάνατο

Αλλά πρέπει να ρίξουν μια λοξή ματιά σε αυτόν

Και έρχονται στροβιλιζόμενα προς τη φλόγα του κεριού –

Πόσο μυστικό είναι αυτό και πόσο προνομιούχος

Νιώθει κάποιος να βρίσκει την ίδια αναγκαιότητα

Κρυπτογραφημένη σε διάφορες μορφές και κατά τα άλλα

Χωρίς συγγένεια –αυτό είναι το ωραίο

Στη Φύση όπως και στην τέχνη, όχι προφανές,

Όχι απρόσιτο, αλλά κάπου ανάμεσα.

Μπορεί να μειώσει λίγο την ξηρή μας απόλαυση

Να αναρωτιόμαστε αν καθετί που είμαστε και κάνουμε

υπόκειται σε κάποιο μικρό νόμο όπως αυτόν,

Κρυμμένο στη φύση, αλλά όχι τόσο βαθιά.

2. ΣΧΟΛΙΑ

2.1 Ένα φιλοσοφικό θέμα που επανέρχεται ξανά και ξανά είναι η διαφορά μεταξύ της προσωπικής μας αίσθησης ότι πράττουμε ελεύθερα (αυτεξούσιο της βουλήσεως) και της αντικειμενικής γνώσης μας ότι συμπεριφερόμαστε σύμφωνα με νόμους και κανόνες που μπορούν να διατυπωθούν με μεγάλη ακρίβεια. Έτσι, στο “Figures of Thought” ο Howard Nemerov μας υπενθυμίζει ότι, καθώς ο πιλότος μαχητικού περικυκλώνει τον εχθρό με ενθουσιασμό για την κατάρριψη, ακολουθεί την ίδια λογαριθμική σπειροειδή πορεία με το ηλιοτροπικό ζουζούνι που ρίχνεται στη φλόγα του κεριού.

2.2 Πολλοί στη σύγχρονη επιστήμη λένε ότι (Δες πειράματα Libet) ο εγκέφαλός μας έχει αποφασίσει περί του πρακτέου λίγο πριν ‘αποφασίσουμε’ εμείς και έτσι δεν υπάρχει ελεύθερη βούληση. Το ερώτημα είναι βάσει ποιων ψυχο-νοητικών μοντέλων αποφασίζει ο εγκέφαλος; Στη συγκεκριμένη περίπτωση αποφασίζει με βάση τη ‘λογαριθμική σπείρα’ που βρίσκεται παντού στη φύση.

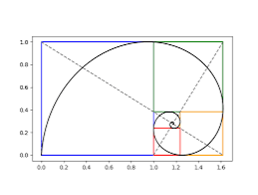
2.3 Εδώ ο ποιητής χρησιμοποιεί μαθηματικά στοιχεία και συγκεκριμένα τη λεγόμενη ‘λογαριθμική σπείρα’. Μια λογαριθμική σπείρα ή ‘σπείρα ανάπτυξης’ είναι μια αυτο-όμοια σπειροειδής καμπύλη που εμφανίζεται συχνά στη φύση. Ο πρώτος που περιέγραψε μια λογαριθμική σπείρα ήταν ο Albrecht Dürer (1525) που την ονόμασε ‘αιώνια γραμμή’.

3. ΠΕΡΑΙΤΕΡΩ ΣΧΟΛΙΑ

3.1 Το ποίημα είναι στοχαστικό και βαθιά φιλοσοφικό έργο που εξερευνά τη φύση της σκέψης, της γλώσσας και της δημιουργικότητας.

[Η Μεταφορική Φύση της Σκέψης] Ο Nemerov χρησιμοποιεί πλούσιες μεταφορές και εικόνες για να απεικονίσει πώς η σκέψη λειτουργεί. Υπονοεί ότι η σκέψη δεν είναι στατική οντότητα, αλλά δυναμική διαδικασία που διαμορφώνεται από τη γλώσσα και τη φαντασία.

[Σχέση μεταξύ Γλώσσας και Πραγματικότητας] Το ποίημα θέτει ερωτήματα σχετικά με το πώς η γλώσσα διαμορφώνει την αντίληψή μας για την πραγματικότητα. Υπογραμμίζει την ιδέα ότι οι “μορφές της σκέψης” είναι ουσιαστικά “μορφές της γλώσσας” και ότι η γλώσσα είναι το μέσο μέσω του οποίου κατανοούμε τον κόσμο.

[Η Δημιουργική Δύναμη της Φαντασίας] Ο Nemerov γιορτάζει τη δύναμη της φαντασίας να δημιουργεί νέες συνδέσεις και να αποκαλύπτει κρυμμένες αλήθειες. Το ποίημα είναι μια μαρτυρία για τη δημιουργική διαδικασία και για το πώς η φαντασία μπορεί να μεταμορφώσει την καθημερινή εμπειρία σε κάτι αξιοθαύμαστο.

[Συνοψίζοντας] Το “Figures of Thought” είναι ποίημα που προσκαλεί τον αναγνώστη να προβληματιστεί για τη φύση της σκέψης, της γλώσσας και της δημιουργικότητας. Είναι έργο που είναι ταυτόχρονα διανοητικό και συναισθηματικό, και παραμένει επίκαιρο και συναρπαστικό.

3.2 Το Figures of Thought του Howard Nemerov είναι μια συλλογή ποιημάτων και δοκιμίων που εξετάζει τη φύση της ποίησης, της γλώσσας και της σκέψης, γραμμένη με το ιδιαίτερο ύφος του Nemerov—συνδυασμός ειρωνείας, σοβαρότητας και βαθιάς στοχαστικότητας. Ο Nemerov, ως ποιητής και δοκιμιογράφος, προσεγγίζει τη γλώσσα όχι μόνο ως εργαλείο έκφρασης αλλά και ως έναν τρόπο κατανόησης του κόσμου. Στο Figures of Thought, διερευνά τη σχέση μεταξύ τέχνης και πραγματικότητας, τον ρόλο της φαντασίας, καθώς και τον τρόπο που η ποίηση αποκαλύπτει τις αλήθειες που η πεζή λογική συχνά αδυνατεί να συλλάβει. Τα δοκίμια του είναι πλούσια σε λογοτεχνικές αναφορές και φιλοσοφικό στοχασμό, αλλά παραμένουν προσβάσιμα χάρη στο κομψό και συχνά παιχνιδιάρικο ύφος του. Αναλύουν τη φύση της ποίησης και της σκέψης με συνδυασμό σοβαρότητας και πνευματώδους χιούμορ.

3.3 Το ποίημα είναι στοχαστικό έργο που εξετάζει τη σχέση ανάμεσα στη σκέψη, τη γλώσσα και την πραγματικότητα. Ο Nemerov συχνά χρησιμοποιεί την ποίησή του για να αναδείξει την ειρωνεία και την πολυπλοκότητα της ανθρώπινης ύπαρξης και αυτό το ποίημα δεν αποτελεί εξαίρεση.

[Ανάλυση του ποιήματος] Το “Figures of Thought” παίζει με τη διττή σημασία του τίτλου του: αφενός αναφέρεται στις μεταφορές και τις μορφές γλωσσικής έκφρασης, αφετέρου υπονοεί τα νοητικά σχήματα και τις ιδέες που διαμορφώνουν την αντίληψή μας για τον κόσμο.

[Κύρια θεματική] Το ποίημα προβληματίζεται γύρω από την έννοια της γνώσης και της κατανόησης. Σκιαγραφεί πώς οι σκέψεις μας δεν είναι πάντα τόσο ακριβείς ή σταθερές όσο θέλουμε να πιστεύουμε—μοιάζουν με σχήματα που μεταμορφώνονται, με νοητικές εικόνες που δεν παραμένουν αναλλοίωτες.

[Υφολογικά στοιχεία] Ο Nemerov χρησιμοποιεί κομψή αλλά συχνά ειρωνική γλώσσα, υπονοώντας ότι η ίδια η πράξη τού να σκεφτόμαστε τον κόσμο είναι ταυτόχρονα δημιουργική και περιοριστική.

[Φιλοσοφικές προεκτάσεις] Το ποίημα φαίνεται να αγγίζει ιδέες από τον πλατωνισμό (όπου οι σκέψεις είναι σκιές των αληθινών ιδεών) αλλά και από έναν πιο σύγχρονο σκεπτικισμό, που αναρωτιέται κατά πόσο μπορούμε ποτέ να γνωρίσουμε πραγματικά κάτι.

[Εντύπωση και σημασία] Το “Figures of Thought” είναι ένα ποίημα που προσκαλεί τον αναγνώστη να στοχαστεί για τη φύση της γνώσης και της αντίληψης. Ο Nemerov, με την ιδιαίτερη μίξη φιλοσοφίας και ποίησης, μας υπενθυμίζει ότι οι σκέψεις μας είναι εύθραυστες και συνεχώς μεταβαλλόμενες—μια θεματική που συναντάται συχνά στο έργο του.

3.4 Στο ποίημά του ο Howard Nemerov χρησιμοποιεί τη λογαριθμική σπείρα ως κεντρικό σύμβολο για να εκφράσει την έννοια της ατέρμονης σκέψης και της ατελείωτης αναζήτησης γνώσης.

[Η σημασία της λογαριθμικής σπείρας] Η λογαριθμική σπείρα είναι μαθηματικό σχήμα που εμφανίζεται συχνά στη φύση (όπως στα κοχύλια, στις τροχιές των γαλαξιών, στις κεραίες των ζώων). Το κύριο χαρακτηριστικό της είναι ότι διευρύνεται χωρίς να αλλάζει τη μορφή της , συμβολίζοντας έτσι την ιδέα της συνεχούς εξέλιξης και της ατελείωτης προσέγγισης μιας αλήθειας ή ενός στόχου .

[Σύνδεση με το ποίημα] Ο Nemerov έχει τη λογαριθμική σπείρα για να περιγράψει τον τρόπο με τον οποίο οι σκέψεις μας εξελίσσονται: πάντα κινούμαστε προς μια αλήθεια, αλλά ποτέ δεν την αγγίζουμε ολοκληρωτικά. Όπως η σπείρα προχωρά προς το κέντρο της αλλά δεν φτάνει ποτέ, έτσι και ο νους αναζητά τη γνώση, αλλά πάντα υπάρχει κάτι ακόμα να μάθει. Το ποίημα μπορεί να διαβαστεί ως στοχασμός πάνω στην ανθρώπινη αντίληψη και την τάση μας να δομούμε την πραγματικότητα μέσα από τα νοητικά μας σχήματα—που, όπως η σπείρα, είναι αέναα εξελισσόμενα.